Classification Tree: 2D Problém

Séria Yalmip & SVM obsahuje:
Yalmip test: Support Vector Machine (2D problém)
Yalmip & SVM: Universal Function
Od separátora ku klasifikácii.

Definícia problému

Máme tri skupiny dát - A, B a C, ktoré chceme klasifikovať. Vieme, že Support Vector Machine algoritmus dokáže v jednom cykle klasifikovať iba dve skupiny dát, t.j. vytvoriť jeden lineárny separátor. Ako teda postupovať pri väčšom počte skupín dát? Odpoveď na túto otázku nájdeme v dnešnom príspevku.

Riešenie problému

Problém budeme riešiť metódou klasifikačných stromov. Postup je nasledovný:

1. Skupinu B a skupinu C spojíme do jednej skupiny BC.
2. Nájdeme prvý separátor medzi skupinou A a skupinou BC.
3. Nájdeme druhý separátor medzi skupinou B a skupinou C.
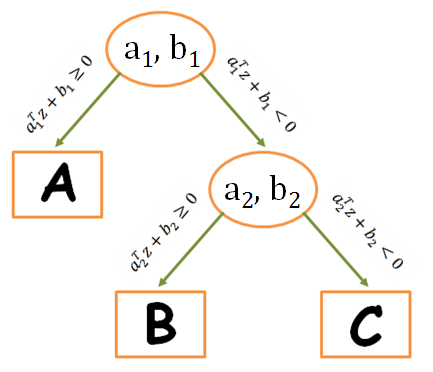
4. Novú vzorku (reprezentovaná vektorom z) vyhodnotíme pomocou série podmienok nižsie.
5. Ak je výraz obsahujúci koeficienty prvého separátora väčší alebo rovný ako nula, vzorka patrí do skupiny A.
6. Ak je takýto výraz menší ako nula, pokračujeme s vyhodnocovaním.
7. Ak je výraz obsahujúci koeficienty druhého separátora väčší alebo rovný ako nula, vzorka patrí do skupiny B.
8. V opačnom prípade vzorka patrí do skupiny C.

Načítame súbor body.mat, ktorý obsahuje vektory A, B a C. Vektor A je rozmeru 2x12, vektor B 2x11 a vektor C 2x14. Pomocou funkcie plot vykreslíme body patriace do všetkých troch skupín dát.

load body.mat
plot(A(1,:),A(2,:),'r+',B(1,:),B(2,:),'b+',C(1,:),C(2,:),'g+')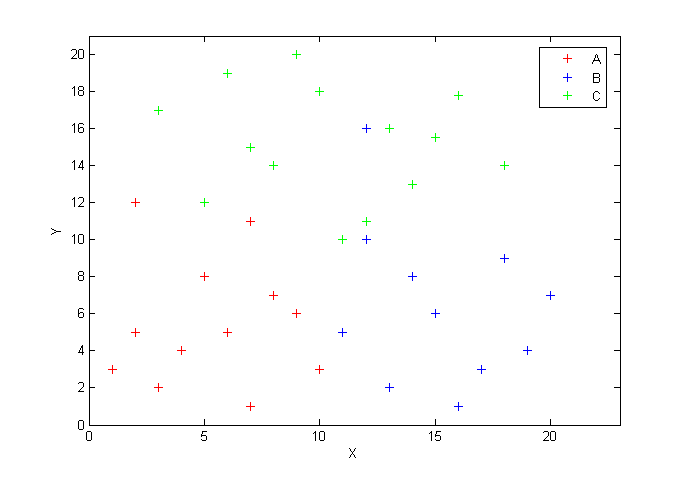

Naformulovaním problému v Yalmipe získame koeficienty prvého separátora. (Vysvetlenie jednotlivých príkazov nájdeme v predchádzajúcom príspevku.)

%% prvý separátor
BC = [B,C];
n1 = size(A,1);
m1 = size(A,2);
l1 = size(BC,2);

gamma = 1;

sdpvar b1; 
a1 = sdpvar(n1,1,'full');
u1 = sdpvar(m1,1,'full');
v1 = sdpvar(l1,1,'full');

objective_function = 1/4*a1'*a1 + gamma*(sum(u1) + sum(v1));

constraints = [u1>=0; v1>=0; 
               a1'*A + b1 >= 1 - u1'; 
               a1'*BC + b1 <= -1 + v1'];

optimize(constraints,objective_function)

opt_a1 = value(a1);
opt_b1 = value(b1);

x = 1:0.1:13;
y = (-opt_a1(1)/opt_a1(2)*x)-(opt_b1/opt_a1(2));
hold on
plot(x,y,'k')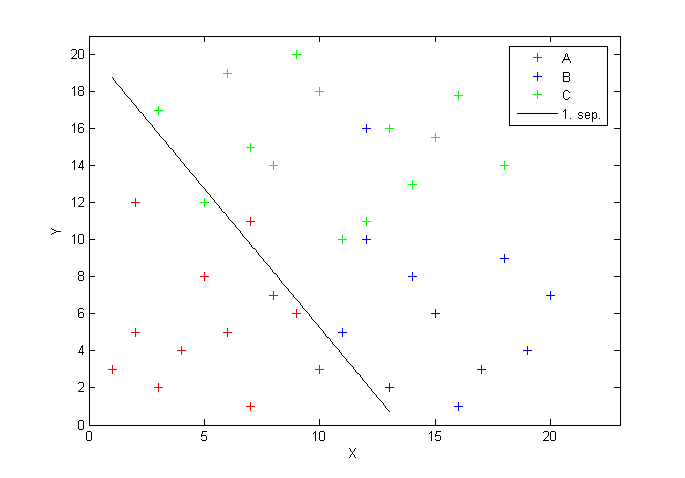

Analogicky získame koeficienty druhého separátora.

%% druhý separátor
n2 = size(B,1);
m2 = size(B,2);
l2 = size(C,2);

sdpvar b2;
a2 = sdpvar(n2,1,'full');
u2 = sdpvar(m2,1,'full');
v2 = sdpvar(l2,1,'full');

objective_function = 1/4*a2'*a2 + gamma*(sum(u2) + sum(v2));

constraints = [u2>=0; v2>=0; 
               a2'*B + b2 >= 1 - u2'; 
               a2'*C + b2 <= -1 + v2'];
           
optimize(constraints,objective_function)

opt_a2 = value(a2);
opt_b2 = value(b2);

Do grafu dokreslíme aj druhý separátor.

x = 8:0.1:20;
y = (-opt_a2(1)/opt_a2(2)*x)-(opt_b2/opt_a2(2));
hold on
plot(x,y,'m')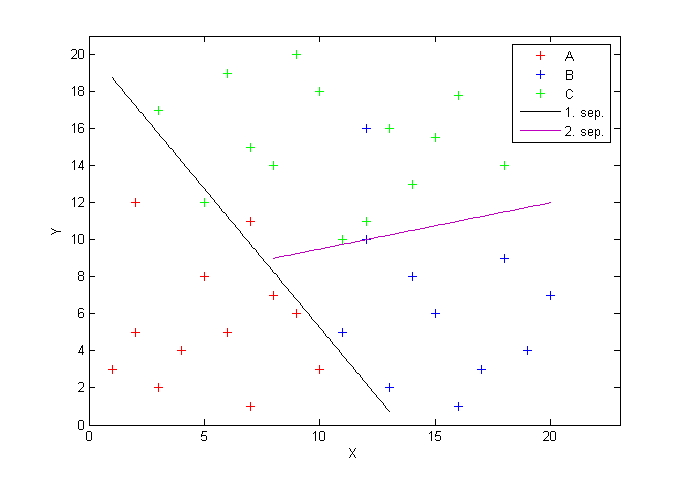

Nové vzorky klasifikujeme nasledovaním pokynov v úvode. (Vysvetlenie príkazov nájdeme v príspevku "Od separátora ku klasifikácii")

%% Klasifikácia
samples = [2 16 18; 9 10 18];

class1 = 'A';
class2 = 'B';
class3 = 'C';

cell_class1 = cellstr(class1); 
cell_class2 = cellstr(class2);
cell_class3 = cellstr(class3);

clmns = size(samples,2);
class = cell(clmns,1);

for i = 1:clmns
    if ((opt_a1'*samples(:,i) + opt_b1) >= 0)
        class(i) = cell_class1;
        
        else if ((opt_a2'*samples(:,i) + opt_b2) >= 0)
                class(i) = cell_class2;
    
        else class(i) = cell_class3;
        end
    end
end

Ako výsledok dostaneme vektor class.

class = 

    'A'
    'B'
    'C'