V posledných desaťročiach si ľudia zvykli, že môžu dostať čokoľvek v priebehu niekoľkých minút, či už hovoríme o potravinách, oblečení, liekoch... Aby sa zabezpečila stálosť kvality tovaru a jeho kapacita na trhu, je potrebné týmto podmienkam prispôsobiť výrobné prevádzky. Jednou z možností je aj automatizácia priemyslu. Avšak aby sa dodržala vysoká kvalita a bezpečnosť danej komodity, je potrebné vytvoriť správny kontrolný systém, ktorý by spĺňal dané požiadavky a tým pádom je nutné výrobný proces dokonale poznať. Na tomto mieste čelíme problému. Aby sme nastavili správne kontrolné mechanizmy, musíme vytvoriť správny matematický model, ktorý môže byť často veľmi zložitý; inými slovami, jeho návrh zaberie veľa času a tým pádom stojí firmu aj veľa peňazí.
Aby sme sa vyhli spomínaným problémom, môžeme namiesto matematických modelov využiť databázové modely, ktoré sú často omnoho jednoduchšie a ich vytvorenie nezaberá toľko času. Jediné čo potrebujeme na návrh dátového modelu, sú vstupné a výstupné údaje z procesu. Tu sa stretávame s ďalším problémom. Údaje z reálnych procesov sú do určitej miery zaťažené šumom a modely získané z týchto údajov sú teda zákonite nepresné. Z tohto dôvodu potrebujeme najskôr signál nejako spracovať.
Dnes máme k dispozícii množstvo metód, ktorými môžeme získaný signál spracovať a jednou z nich je aj „garantovaný odhad parametrov“.
Ako funguje metóda garantovaného odhadu parametrov (GPE) si ozrejmíme na nasledujúcom príklade. Predstavme si, že sme získali údaje z procesu, ktoré v tomto prípade budú predstavovať funkciu s konštantnými hodnotami. Vieme, že senzor má stanovenú chybu merania. Matematický predpis procesu, z ktorého sme získali údaje, nepoznáme a preto sa rozhodneme, že budeme tieto údaje aproximovať lineárnou funkciou a taktiež budeme chcieť, aby výsledná priamka ležala v rozmedzí hraníc chyby merania senzora. Keďže poznáme vstupné a výstupné údaje, jediné neznáme v rovnici sú úsek a smernica. Vyjadrime si napríklad smernicu (P2) ako funkciu úseku (P1) a pre každý nameraný údaj zostrojíme dve priamky, kde vo výstupnom údaji (závislá premenná) je zohľadnená extrémna hodnota chyby merania. Tieto priamky vytyčujú oblasť vhodných kombinácií parametrov modelu, smernice a úseku, ktorými môžeme opísať dané dáta a garantuje, že správne riešenie leží niekde vo vnútri tejto oblasti.
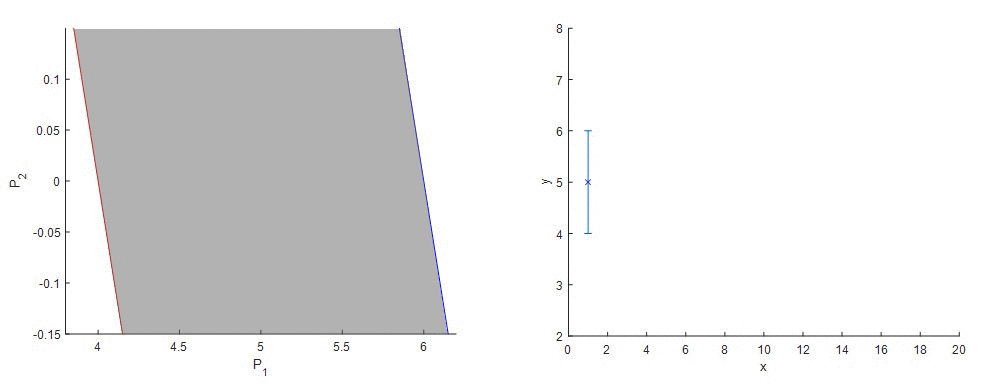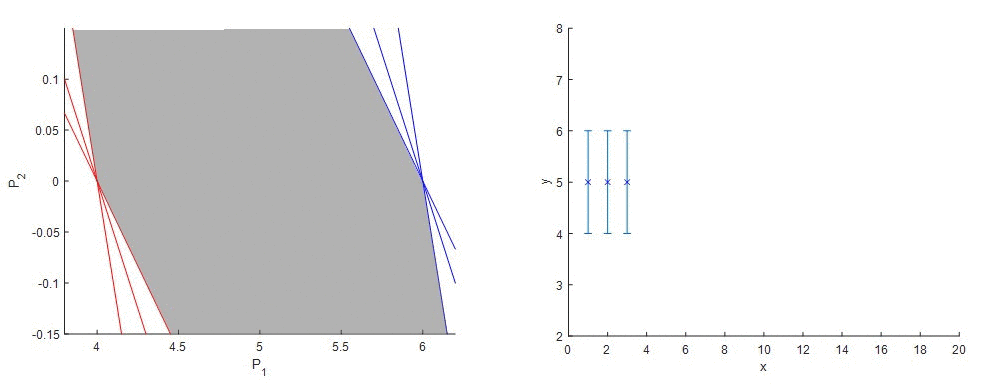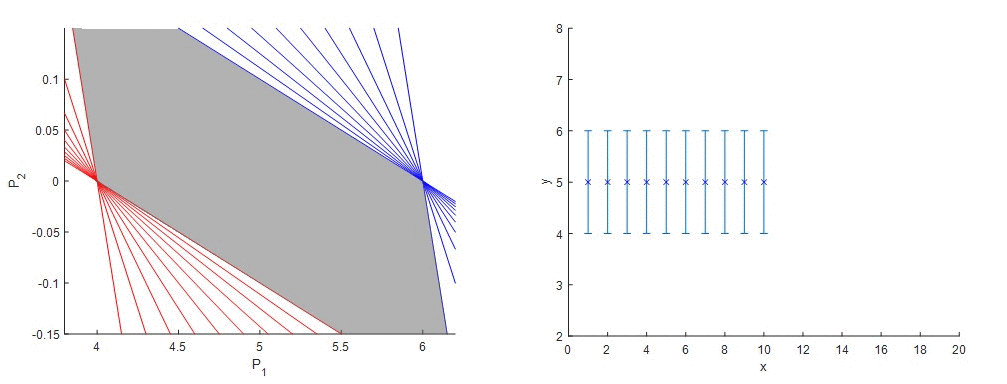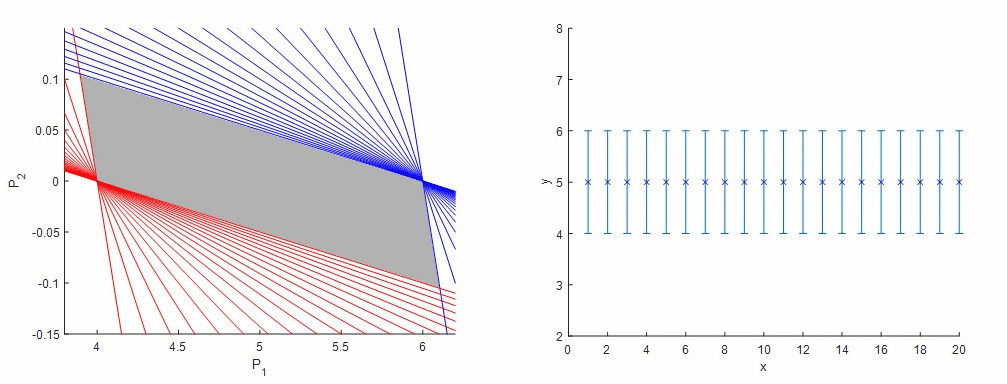
Obr. 1 - Metóda Garantovaného odhadu parametrov - lineárna regresia nameraných údajov (idealizované).
Takto sme nielen získali informácie o parametroch modelu, ale aj informácie o zložitosti resp. jednoduchosti modelu. Na obr. 1 vidíme, že parameter P2, teda smernica priamky, obsahuje vo svojom intervale nulu, a tým pádom pre niektoré kombinácie parametrov by sme získali smernicu nulovú – náš lineárny opis je teda potenciálne zbytočne zložitý a dané dáta môžu byť dobre opísané aj konštantnou funkciou.
V predchádzajúcom príklade sme uvažovali merané dáta, ktoré boli zidealizované t.j. senzor v každom bode nameral rovnakú hodnotu, žiaden šum sa nezaznamenal. Ak by naše merania obsahovali šum a predpokladali by sme rovnaký postup ako v predošlom príklade, výsledok by bol viac menej rovnaký s tým rozdielom, že odhadovaný interval hodnôt parametrov sa zmenší.
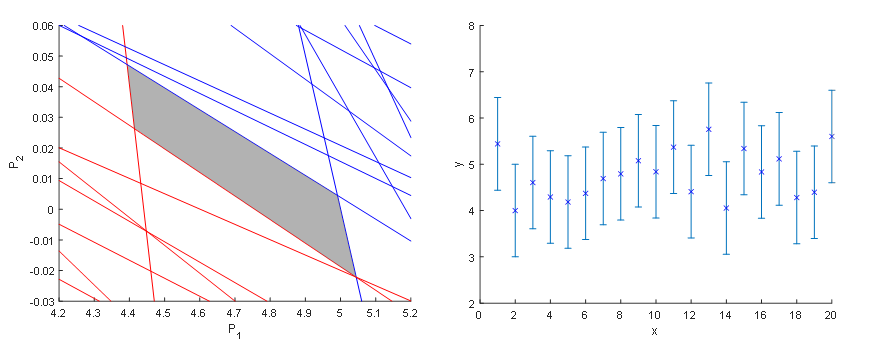
Obr.2 - Metóda Garantovaného odhadu parameterov – lineárna regresia nameraných údajov so šumom.
Máme teda relatívne jednoduchú metódu, ktorou dokážeme získať informácie o parametroch a zložitosti modelu a tieto vlastnosti využijeme pri identifikácii dátových modelov, najmä pri určovaní rádu modelu, pričom táto problematika je omnoho zložitejšia ako problematika určenia parametrov modelu.
Celý semestrálny projekt sme venovali pozornosť FIR („Finite Impulse Response“) modelu. FIR model je lineárny model v diskrétnom čase, ktorý môžeme vyjadriť nasledovne:
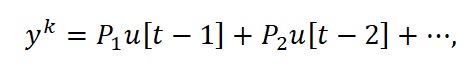
kde počet koeficientov určuje rád modelu. Ak chceme získať dynamický model, ktorý by adekvátne opisoval namerané dáta potrebujeme vyriešiť optimalizačnú úlohu hľadania minimálneho rádu modelu. Problematika je rovnaká ako na začiatku, keď sme sa snažili opísať namerané údaje neznámeho charakteru lineárnou priamkou. Máme k dispozícii dáta z neznámeho procesu, lenže nepoznáme počet a ani hodnoty parametrov modelu, ktorý by dokázal tieto dáta aproximovať. Takže začneme modelom 1. rádu a vyjadríme si neznámy parameter modelu P1 ako funkciu vstupných a výstupných údajov, kde každý výstupný údaj opäť zohľadňuje extrémnu hodnotu chyby merania. Ak po použití všetkých nameraných údajov získame pre daný rád modelu nejakú ohraničenú oblasť vhodných parametrov, potom sme našli minimálny rád modelu. Ak takúto oblasť nenájdeme musíme zvýšiť rád modelu. Tento optimalizačný problém sme vyriešili lineárnym programovaním, ktoré nám nahradilo grafickú metódu. Aby sme vedeli posúdiť zložitosť modelu daného rádu, potrebovali sme intervalový odhad všetkých parametrov t.j. ich minimálnu a maximálnu hodnotu. V princípe budeme hľadať vrcholy oblasti, ktorú získame tiež tou istou metódou ako v predchádzajúcej optimalizačnej úlohy, lenže ako náš FIR model naberá na zložitosti resp. počte parametrov, táto problematika sa stáva viacrozmernou a tým pádom by bola zložitá na grafické riešenie. Túto problematiku sme opäť riešili lineárnym programovaním.
Cieľom tejto práce bolo získať model, ktorý dokáže čo najlepšie aproximovať získané dáta a priblížiť sa k reálnym výstupom procesu t.j. priebehu bez šumu. Okrem spomínanej filtračnej vlastnosti, dátové modely disponujú aj predikčnou vlastnosťou, ktorá môže byť istým ukazovateľom kvality modelu.
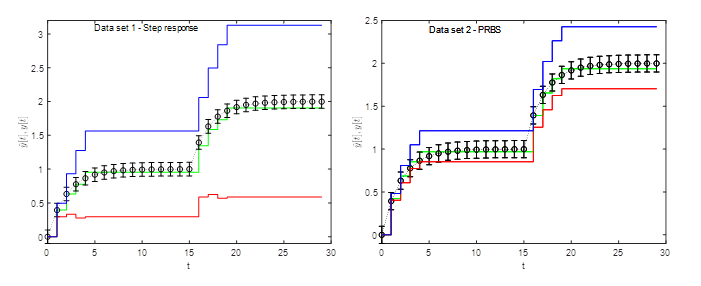
Obr. 3 - Porovnanie predikčných vlastností FIR modelov získaných z údajov z prechodovej funkcie 1. rádu so zosilnením Z = 8 a časovou konštantou T = 2, vybudených na rôznych vstupných signáloch – skoková zmena (Data set 1), PNBS (Data set 2). Čierna – reálny priebeh prenosu pri 2 skokových zmenách; Zelená – optimálne riešenie; Modrá – maximálna realizácia; Červená – minimálna realizácia.
Na Obr. 3 môžeme vidieť priebehy dvoch rôznych modelov, ktoré boli trénované na odlišných dátach. Obrázok vľavo predstavuje FIR model natrénovaný na dátach z prechodovej funkcie 1. Rádu so zosilnením Z=8 a časovou konštantou T=2, ktorá bola vybudená skokovou zmenou. Obrázok vpravo predstavuje podobný FIR model s tým rozdielom, že dáta, na ktorých bol model natrénovaný, pochádzali z prechodovej funkcie vybudenej pseudonáhodnou binárnou sekvenciou (PRBS). Môžeme usúdiť, že model trénovaný na PRBS je po kvalitatívnej stránke výrazne lepší. Okrem toho, že je bližšie k reálnej hodnote, akú by nadobúdal samotný proces, tak aj rozptyl minimálnej a maximálnej realizácie výstupu je omnoho menší, čiže máme menšie ohraničenie reálneho priebehu dát.
Ďalším ukazovateľom, na základe ktorého môžeme posudzovať kvalitu modelu je tzv. „Pareto front“. Pomocou Pareto frontu sme zobrazili prefitovanie modelu ku jeho presnosti vzhľadom na rád modelu. V rámci semestrálneho projektu sme sa zaoberali aj porovnaním výsledkov z Pareto frontu a štandardných kritérií. Týchto kritérií je niekoľko – AIC (Akaike information criterion), BIC (Bayesian information criterion) a AICc (AIC s korekciou); a dávajú do súvisu presnosť modelu vzhľadom na jeho rád. Aby sme mohli tieto metódy porovnať, museli sme zostrojiť sériu testov pre dva typy modelov, kde sme menili veličiny ako zosilnenie šumu a rozdelenie šumu. Jeden z modelov aproximoval dáta získané z FIR modelu, ktorý bol vybudený pseudonáhodnou binárnou sekvenciou a druhý z modelov bol trénovaný na dátach z procesu opísaného prenosom 1. rádu so zosilnením Z=8 a časovou konštantou T=2 excitovaný taktiež PRBS.
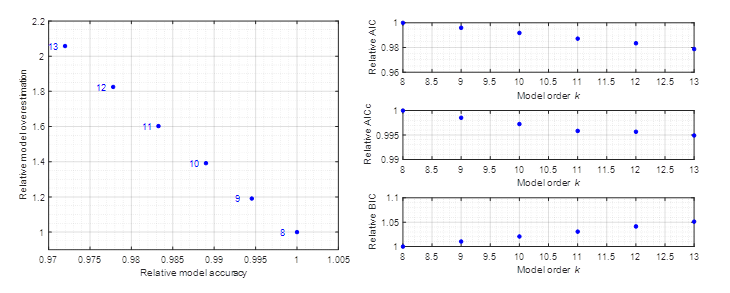
Obr. 4 - Porovnanie Pareto frontu (naľavo) a štandardných kritérií (napravo) modelu natrénovanom na dátach z FIR modelu 8. rádu vybudeného so PRBS.
Z výsledkov sme zistili, že zosilnenie šumu a jeho rozdelenie nemali výrazný kvalitatívny vplyv na jednotlivé metódy. Ale ako si môžeme všimnúť na obr. 4, štandardné kritéria neponúkajú jednotné riešenie pre výber rádu modelu (najlepší = minimum na grafe). Naproti tomu Pareto front ukazuje, že ak by sme chceli o trošku zlepšiť presnosť modelu, získali by sme model s rádovo väčším prefitovaním. Preto ako najlepšia možnosť sa javí model 8. rádu.
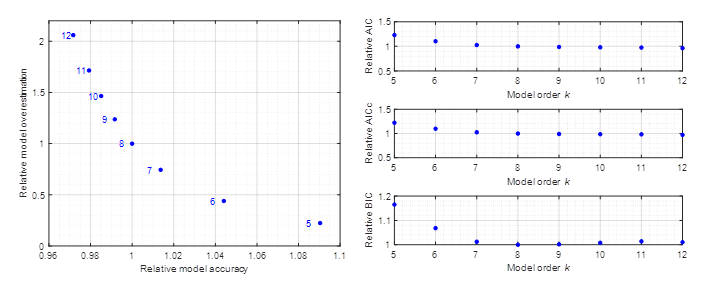
Obr. 5 - Porovnanie Pareto frontu (naľavo) a štandardných kritérií (napravo) modelu natrénovanom na dátach z prechodovej funkcie 1. rádu so zosilnením Z = 8 a časovou konštantou T = 2 vybudenej so PRBS.
Pri študovaní výsledkov modelu trénovanom na údajoch z prenosu procesu 1. rádu si možno všimnúť nasledovné. Podobne ako v prvom prípade aj tu štandardné kritéria dávajú nejasné výsledky a ukazujú, že model 7. až 12. rádu môžu byť rovnako dobré. Naproti tomu na Pareto fronte sa ukazuje, že ak by sme postupne zvyšovali rád modelu, teda presnosť modelu, prefitovanie modelu by nám až tak nestúpalo až po kým nenarazíme na lineárnu pasáž (model 7. alebo 8. rádu), kde každé zlepšenie v presnosti modelu by už znamenal veľký prírastok v prefitovaní.
Získať dátový model, ktorý by dobre opisoval namerané údaje, sa na prvý pohľad nemusí javiť náročne, ale ako sme ukázali, problematika s tým spojená je relatívne komplikovaná. Vysvetlili sme jednoduchú metódu garantovaného odhadu parametrov, ktorá nám nielenže ponúka informácie o parametroch modelu, ale taktiež poskytuje informácie o zložitosti modelu. Avšak verifikácia správnosti modelu sa zdá byť komplikovanejšia záležitosť, najmä ak každá metóda ponúka iný výsledok, čo bolo v prípade štandardných kritérií, zatiaľ čo metóda s Pareto frontom poskytuje jasné a konzistentné výsledky.