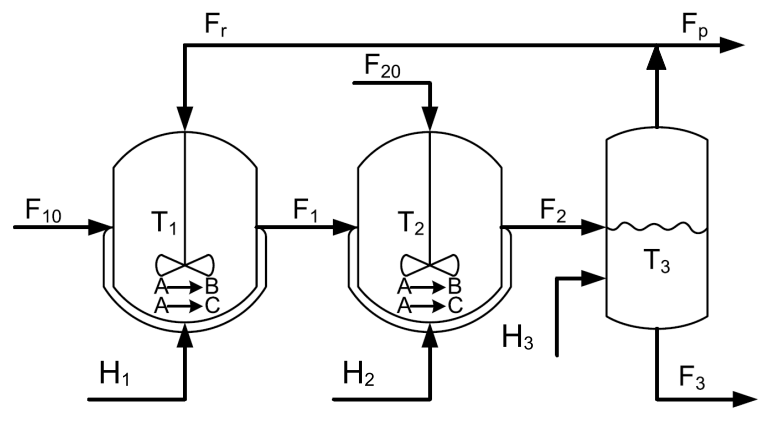
Model Predictive Control (MPC) is an advanced control technique which can be used in chemical plants. It allows quick decision-making and taking the right actions when faced with changing requirements and unexpected events. However, solving a complex problem within limited time is computationally and time-consuming. To solve this, most systems can be divided into symmetrical subsystem, which can be solved in parallel using distributed optimization methods. The control was performed on the reactor-separator plant (Figure 1.).
The process consists of three-vessel, two continuously stirred tank reactors and a tank separator. In the reactors, two reactions are ongoing. The first one is a conversion of the reactant A into the main product B and the second is conversion of A into side-product C. The aim is to regulate the state variables: temperatures and the concentrations of the reactant A and products B and C to the optimal setpoint in each reactor and separator. The control inputs are heat flows H1, H2 and H3, representing the external heat delivered or removed from the tanks.
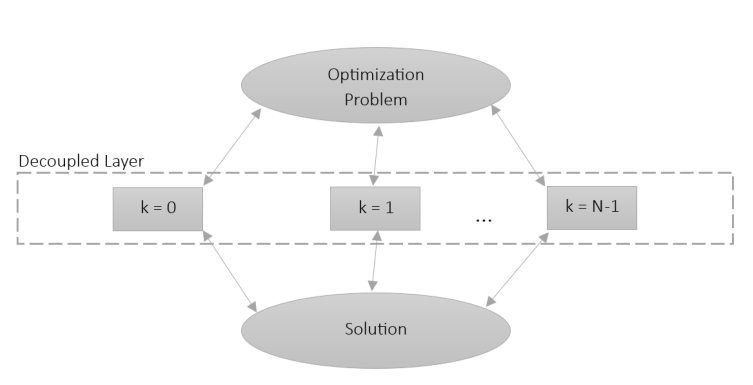
The aims of the project are to design an optimal control for given model using centralized MPC, distributed optimization and then simplify the control problem. Distributed optimization is an optimization method that is often used in large-scale systems. It is based on the decomposition of a problem to several other subproblems. The subproblems are distributed to agents, where computations are performed independently. The results are then exchanged which leads to global solution (Figure 2).
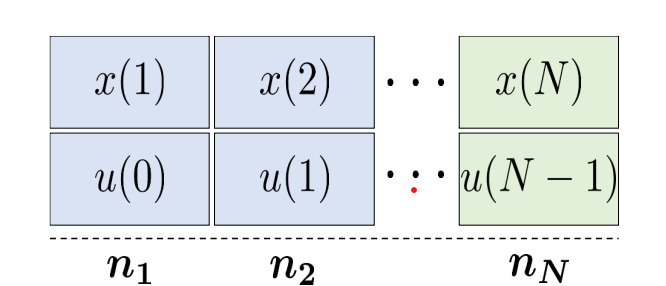
Our studied system was divided into symmetrical subproblems using Augmented Langrangian based Alternating Direction Inexact Newton Method, shortly ALADIN, which is a general method for solving distributed optimization problems, introduced in 2016. When centralized MPC is distributed into separate control steps within the predictive horizon. Then, the cost function is split into individual cost functions. This approach increases the solving agents (Figure 3.).
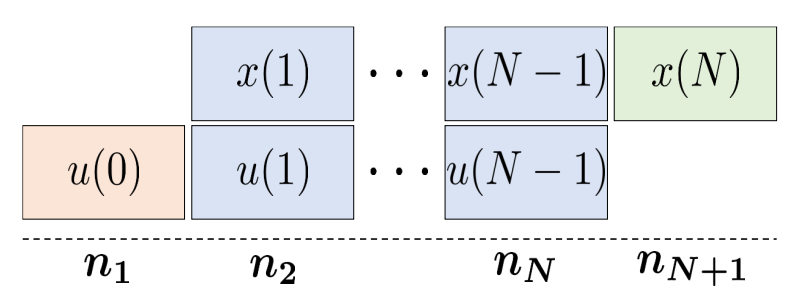
By introducing a simple shift in the cost function, it is possible to lower the number of decoupled subproblems. This approach also simplifies our control problem (Figure 4.).
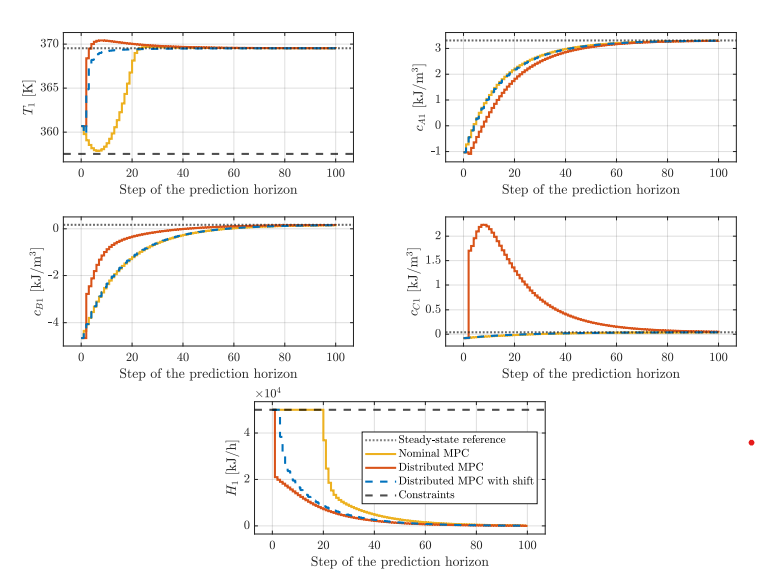
After implementing the centralized MPC, distributed optimization (ALADIN) and simplified control problem, the simplified control problem results are close to the centralized MPC, so we assume that this change in the cost function was successful (Figure 5.).