Our journey to find the best classifier is not yet at the end. The last introduced classifier was the naive Bayes and now the next one – support vector machine itself – has a difficult task to win this competition. The naive classifier set a high bar. Spoiler: the support vector machine (SVM) won only in the one, infamous category – the longest waiting for the results.
But first a brief introduction. Let’s plot each sample (from two classes) as a point in n-dimensional space, where n is number of features (in our case n = 13). Then, a classifier’s job is to find the right hyperplane that segregate the two classes well. But which hyperplane differentiate the two classes best? In a trouble-free case, we have all items from the first class on the one side of that plane and all items from the second class on the other side. If there exists a lot of hyperplanes, we choose the best one – that one where distances between hyperplane and nearest data point on each side are maximized. If such a hyperplane even exists. In some cases, it is better (sometimes it is inevitable) to ignore outliers and find the hyperplane with the largest gap, regardless of the correct classification of all samples.
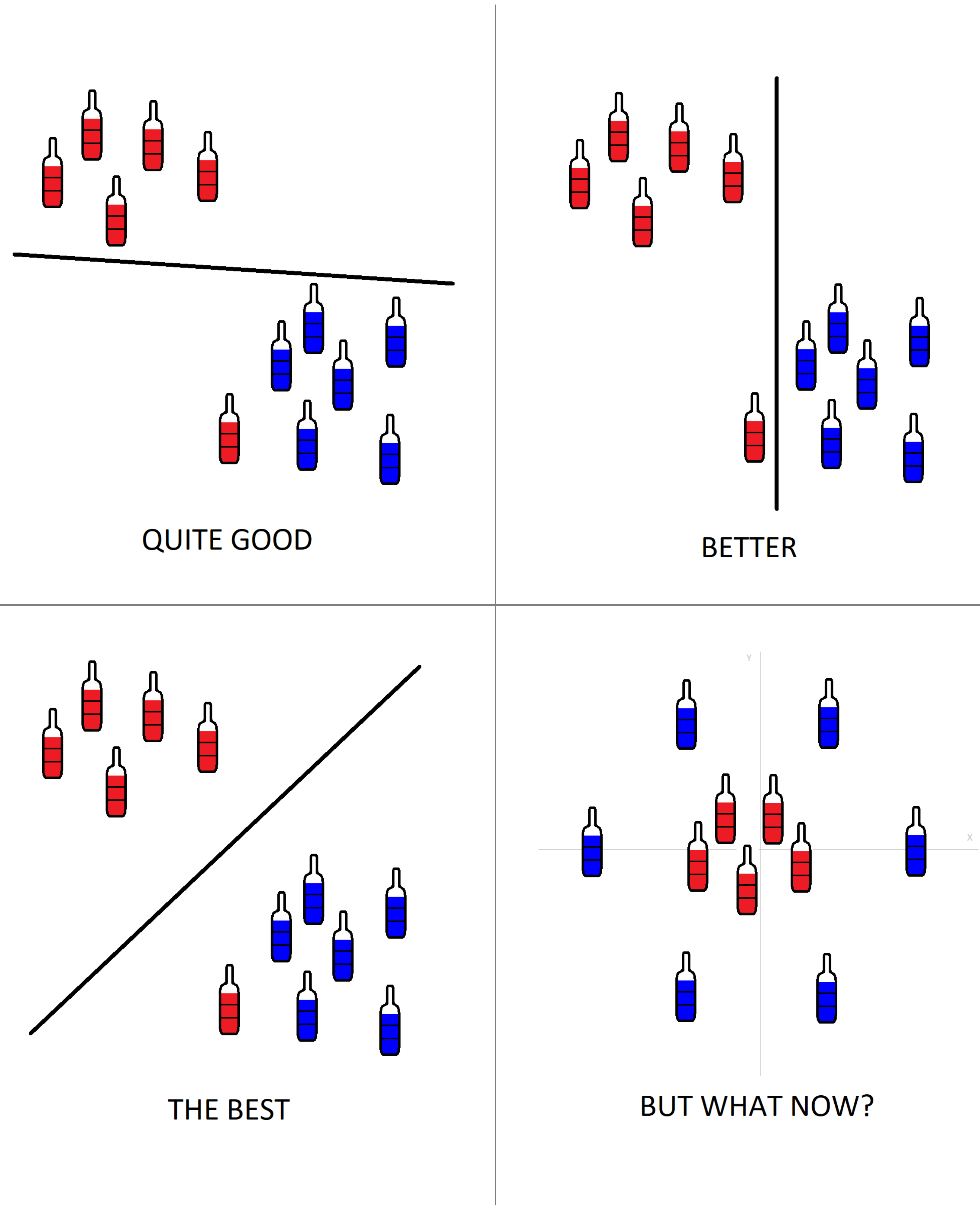
The case in the bottom-right corner looks linearly inseparable, but SVM knows some tricks how to convert it into a separable task. Just add another dimension, great! Kernel functions are able to do these things.
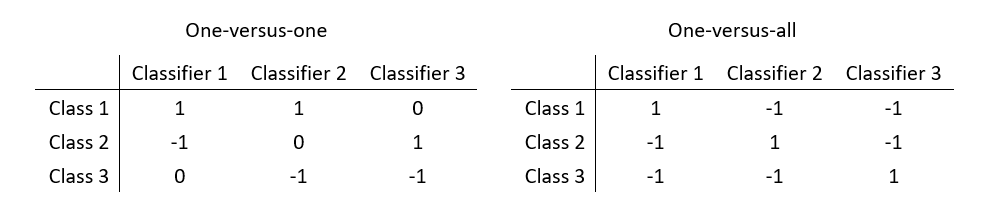
So, only one problem left. Despite SVM is powerful, it can separate only 2 classes at once. Several methods can help and here we’ll use the error-correcting output codes (ECOC) technique. ECOC isn’t very sophisticated, it just uses more SVM classifiers. ECOC classification requires a coding design, which determines the classes that the binary classifiers train on. A coding design is a matrix, where each row corresponds to a class, each column corresponds to a binary classifier and every element of the matrix must be -1, 0, or 1. In our case of three classes we will use three binary classifiers (although, theoretically, two would be enough). If a coding design is type one-versus-one (see the table below). The first classifier will separate classes 1 and 2, the second classifier will separate the classes 1 and 3, and the third classifier will separate class 2 from class 3. ECOC model can somehow combine them and correctly assign a new observation. Another type of a coding design – one-versus-all - works similarly. The first classifier will separate class no. 1 from the rest, the second classifier will separate class 2 from the rest, and the third classifier will separate the class 3 from the rest. To find which type suits better is a task for optimization.
To read a documentation of used function (fitcecoc) before running whole program is a good habit. There is a wise recommendation to standardize the predictors. This saved me a lot of time and the results might be also better. With standardized predictors, hyperparameter optimization lasted about half the time less – “only” 32 hours, continually. The most important data are summarized in the table below.
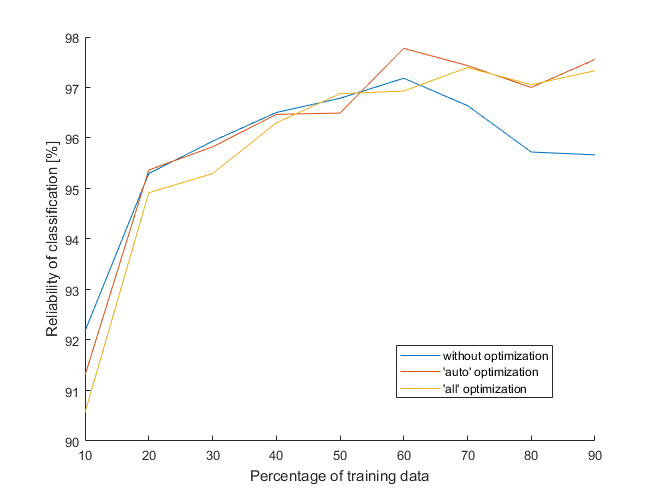
| Mode | Time per one SVM | Reliability at 70 % | Reliability at 80 % |
| without optimization | 0.07 s | 96.6 % | 95.7 % |
| 'auto' optimization | 112.37 s | 97.4 % | 97.0 % |
| 'all' optimization | 145.63 s | 97.4 % | 97.1 % |
The results aren’t bad, they are similar to the previous classifier. But I am not sure whether they are worth so much time. The only scenario worth considering is the one without hyperparameter optimization, because additional optimization doesn’t seem to help much. In the next post, I will try one more classifier and compare them all. Lastly, if you missed the math in this post, here it is:
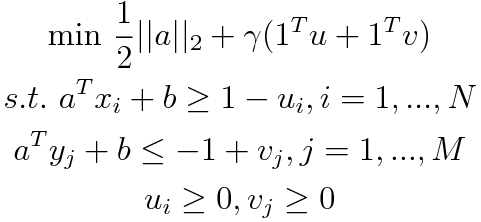
SVM tries to combine the widest gap and the least number of items with wrong classification, with the ratio between these two factors given by the constant $\gamma$. To find the widest gap, a distance between the separating hyperplane and the classified items needs to be maximized (or minimized in its inverse value). Variables $u$ and $v$ create a soft-margin, which allow some points to be on the wrong side if there is no other way. The task is to find the best parameters $a$ and $b$ that determine the separating hyperplane.