Laktóza. Mnohí ju doslova neznášajú, mnohí ju každodenne potrebujú. Používa sa totiž ako najbežnejší nosič liečiv či už v klasických tabletkách alebo inhalátoroch. Cesta od kravičky až k čistej práškovej laktóze je síce dlhá, no jedným z krokov na tejto ceste je aj tzv. membránová separácia, pri ktorej sa srvátka—„voda“ po vyzrážaní (kľaganí) syra—zbavuje prebytočnej vody (H2O) a jednomocných minerálov (napr. NaCl) prirodzene obsiahnutých v mlieku, a tak sa následné získavanie laktózy stáva ešte jednoduchším a lacnejším.
Pórovitú membránu si môžete predstaviť ako sito, ktoré zachytáva častice väčšie ako priemer pórov—proteíny, sacharidy, ťažké kovy—a prepúšťa vodu s malými časticami—napr. soli a menšie organické látky.
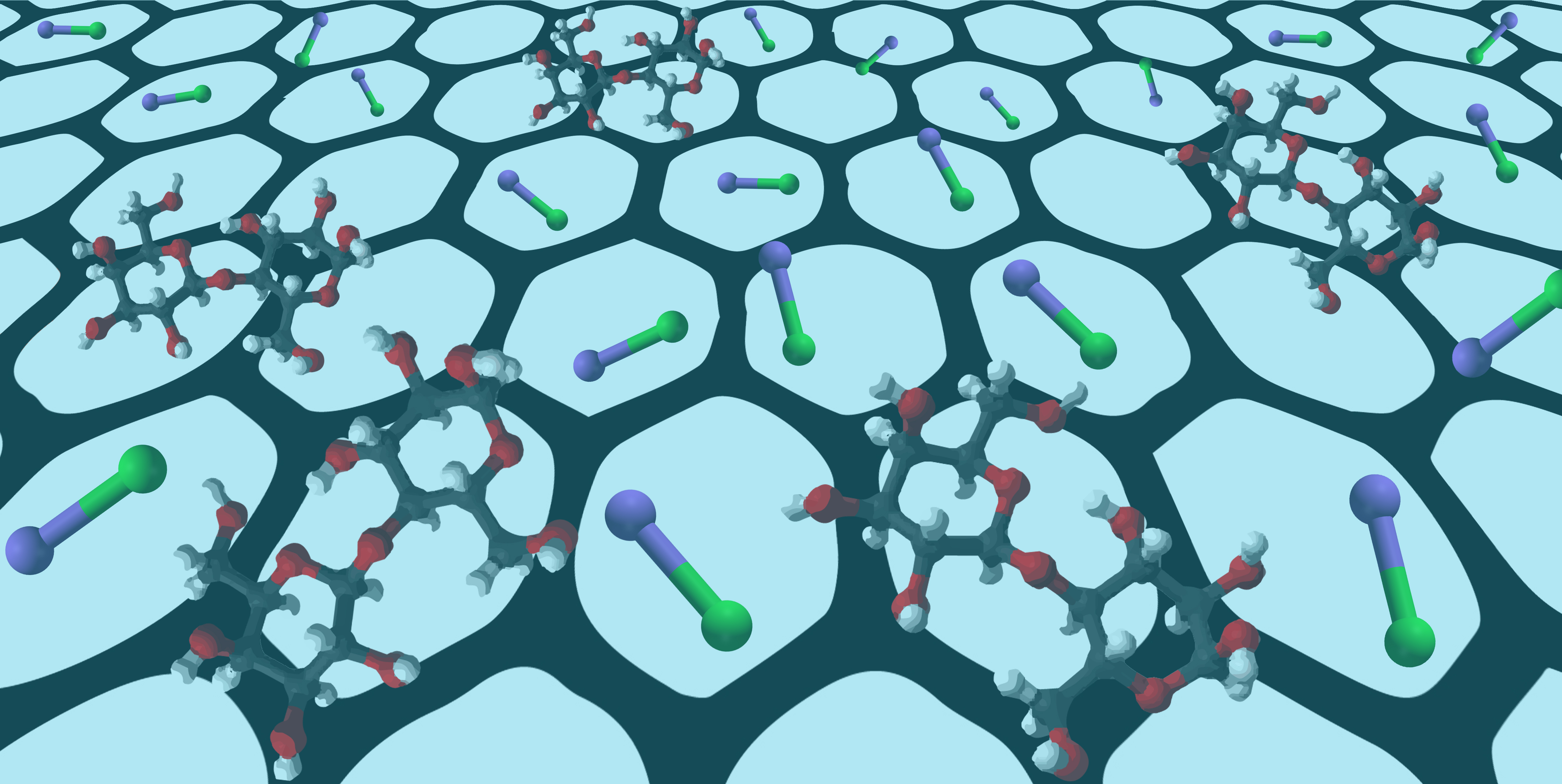
Ak chceme skoncentrovať roztok „veľkého“ cukru a prečistiť ho od „malej“ soli, zvyčajne volíme stratégiu, pri ktorej tento roztok najprv filtrujeme cez membránu—čím ho zbavujeme vody a soli—a následne popri tejto filtrácii ešte dodávame úplne čistú vodu—čím sa iba vymýva soľ. Takýto (aspoň dvojkrokový) proces sa nazýva diafiltrácia a okrem spomínanej srvátky sa používa aj pri výrobe (chutnejšieho) nealko piva vymývaním etanolu z klasického piva alebo pri výmene organických rozpúšťadiel v chemickej výrobe.
Proces diafiltrácie zeleného fluorescenčného proteínu
Súčasný trh nám nedovoľuje šafáriť s časom ani s peniazmi. Voda, ktorá sa používa pri vymývaní solí, zvyčajne pochádza z iného membránového procesu—reverznej osmózy—a býva rádovo stokrát čistejšia, no desaťkrát drahšia ako voda z kohútikov. Ako by ste teda zabezpečili, aby nám diafiltrácia trvala čo najkratšie a aby sme pri nej minuli čo najmenej čistej vody? Ako môžete predpokladať, najlepšia cesta z bodu A do bodu B vedie cez nejaký tretí bod X. V prípade diafiltrácie to napríklad znamená, že v bode X bude koncentrácia laktózy dokonca ešte vyššia ako v konečnom bode B—po skončení vymývania sa roztok jednoducho rozriedi priliatím potrebného množstva vody. Ak vieme správne určiť bod X a rýchlosť vymývania soli, bude nám filtrácia trvať kratšie a celkovo minieme menej vody, ako keby sme neprekročili bod B.
I built a BRACHISTOCHRONE with @tweetsauce! Video: https://t.co/rC5oktUATG @braincandylive pic.twitter.com/sj1FVgqf5v
— Adam Savage (@donttrythis) 22. januára 2017
Modelovanie. Nemusíte si za tým predstaviť plastelínu alebo AutoCAD, v prípade matematického modelovania procesu totiž ide o zostavenie rovníc popisujúcich fyzikálno-chemické zákonitosti, ktorými sa daný proces riadi. Aby sme vedeli matematicky modelovať diafiltráciu spomenutého roztoku laktózy a soli, potrebovali sme najprv namerať dostatočné množstvo dát na reálnej nanofiltračnej stanici. Z týchto dát sme potom vyhodnotili parametre (konštanty) rovníc, ktoré sa na modelovanie filtrácie bežne používajú. Taktiež sme navrhli novú rovnicu, aby sme zistili, či presnejší matematický popis výrazne zlepší „optimálnosť“ procesu. Po modelovaní sme navrhli optimálnu stratégiu a porovnali ju pre dva modely. Jeden model teda zohľadňuje tradične používanú rovnicu (prechodu látky cez membránu) a druhý nami navrhnutú.

(samotné valcové membránové moduly sú: strieborný—nanofiltrácia—a dva biele—reverzná osmóza)
Kontrolou správnosti modelovania a optimalizácie bola prípadová štúdia takého roztoku, ktorého koncentrácia cukru sa zvýši a koncentrácia soli zníži, tak ako bolo spomenuté už vyššie. Ide teda o cestu z A do B, avšak pre dve rôzne rovnice prechodu látky dávajúcu rôzne body X. Simuláciou a experimentom sme zistili, že nami navrhnutý model poskytol asi o 20% rýchlejšiu stratégiu ako tradičný model, keď sme sledovali optimalizáciu z hľadiska času procesu. Spotreba vody bola pri tradičnom modeli síce nižšia, no tá pre jednoduchosť do optimalizácie zahrnutá nebola.
Ukázalo sa teda, že je výhodné poznať presnejší matematický model optimalizovaného procesu, hoci takýto model môže byť oveľa komplikovanejší ako bežne používané modely. Pre prax je výhodné zaoberať sa modelovaním a optimalizáciou, pretože aj malá zmena veličín ovplyvňujúcich proces môže výrazne znížiť jeho celkové náklady.