Ak ste už niekedy hrali šach proti skúsenému protivníkovi, tak viete aké náročné je dosiahnuť pre vás vyhovujúci výsledok. Dvojúrovňová optimalizácia je ako taká šachová partia, kde jedna strana sa snaží minimalizovať funkciu a druhá jej to kazí svojimi ťahmi v podobe maximalizácie. V rámci semestrálneho projektu som sa zaoberal štúdiom metód dvojúrovňovej optimalizácie. Ako príklad som použil problém v princípe podobný šachovej partii, v ktorom som sa snažil umiestniť elipsu daných rozmerov, čo najnižšie nad danú parabolu. Na ľavom obrázku si môžete všimnúť príklad počiatočnej pozície elipsy a na pravom obrázku je očakávaný výsledok.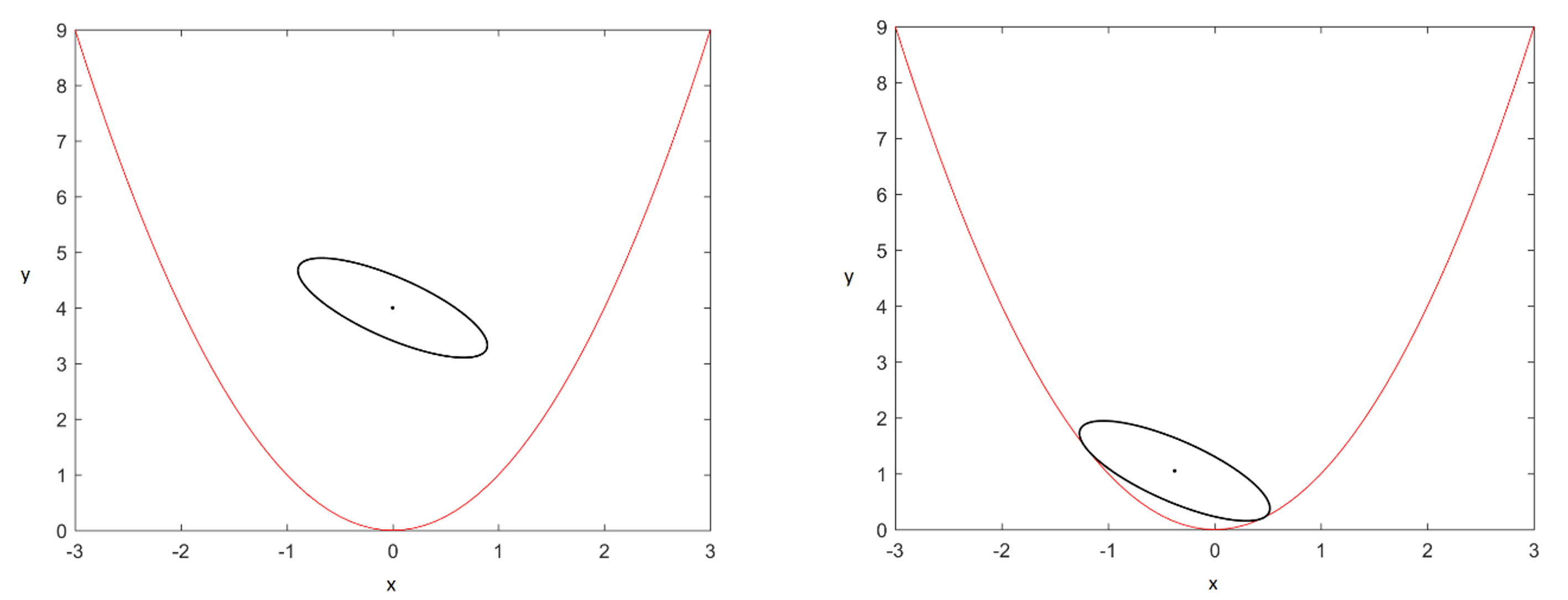
Môj optimalizačný problém je definovaný nasledovne:
V tomto tvare sa jedna o tzv. semi-infinitný problém čo znamená, že problém ma nekonečne veľa obmedzení. Preto bola nutná nasledovná úprava:
Kde Q je kovariančná matica elipsy, ktorá definuje natočenie elipsy. Jeden hráč (minimalizácia) hýbe stredom elipsy a druhý hráč (maximalizácia) sa snaží nájsť bod, ktorý bude čo najviac „trčať“ pod parabolou.
Prvá metóda ktorú som použil funguje presne ako šachová partia, ale obaja hráči (min,max) sa vždy sústredia iba na súčasný krok a všetko, čo bolo predtým alebo čo by mohlo byť po tomto kroku ich nezaujíma. Funguje nasledovne:
- Určíme si vhodný nástrel pre minimalizáciu (hodnoty v,w)
- Vyriešime minimalizáciu a dosadíme hodnoty x,y do maximalizácie
- Vyriešime maximalizáciu a skontrolujeme, či je dané riešenie vhodné (dosadíme nové v,w do ohraničenia minimalizácie a nerovnosť musí platiť)
- Ak nie je vhodné dosadíme do minimalizácie nové hodnoty v, w
- Opakujeme cyklus kým nemáme optimálne riešenie alebo ďalšie opakovanie nemá zmysel.
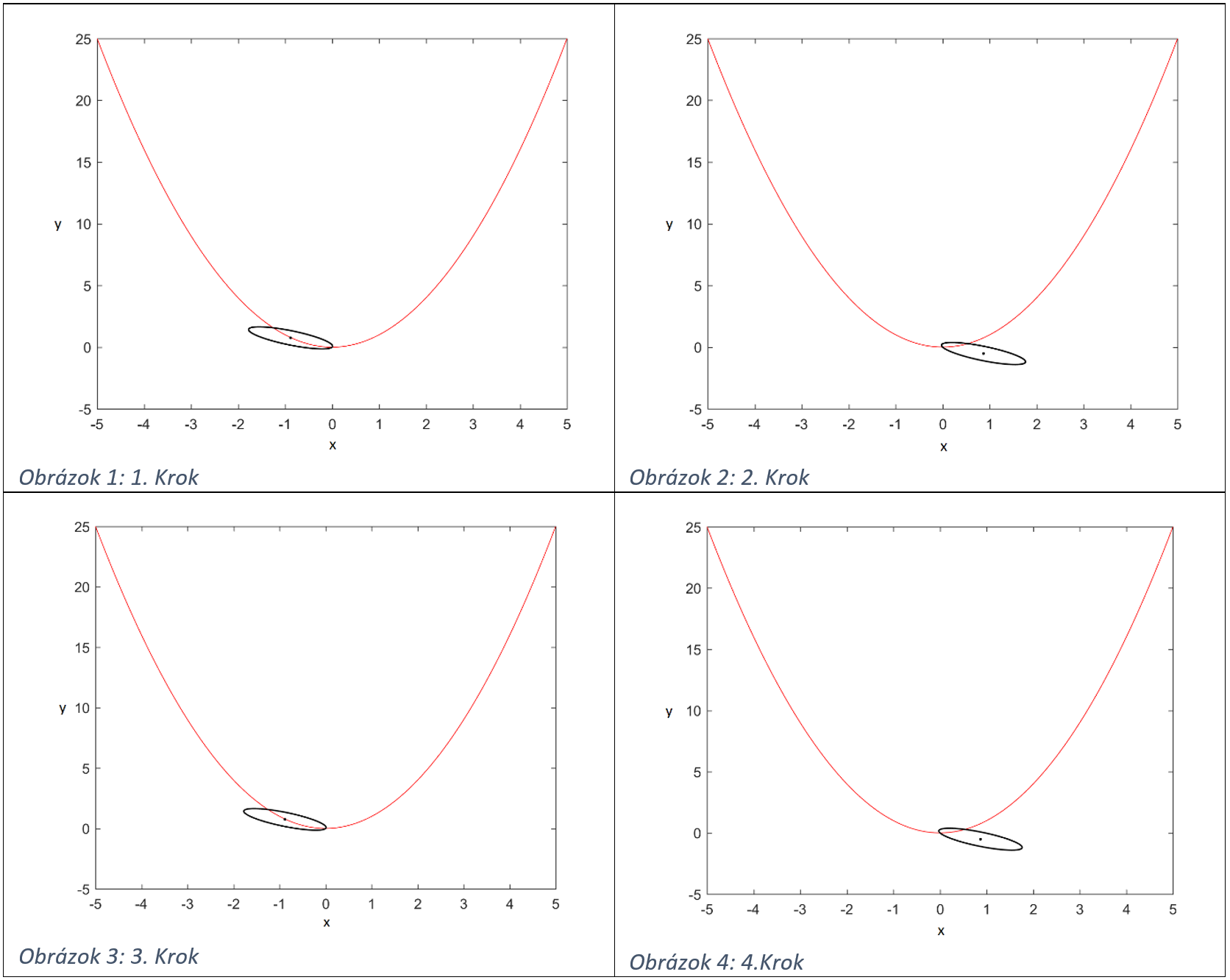
Ako si môžete všimnúť pozícia elipsy v prvom a treťom kroku sa nápadne podobá. Je to spôsobené práve tým, že ani maximalizácia a ani minimalizácia si nepamätajú výsledky v predchádzajúcich krokoch a potom skĺzavajú do opakovania. Piaty, šiesty až n-tý krok by potom vyzeral rovnako ako 3. a 4. krok.
Druhá metóda pomenovaná podľa jej autorov Blankenship a Falk [1] je veľmi podobná alternujúcej metóde, ale má v sebe zakomponovaný práve chýbajúci pamäťový prvok. Funguje nasledovne:
- Určíme si vhodný nástrel pre minimalizáciu (hodnoty v,w)
- Vyriešime minimalizáciu a dosadíme hodnoty x,y do maximalizácie
- Vyriešime maximalizáciu a skontrolujeme či je dané riešenie je vhodné (dosadíme nové v,w do ohraničenia minimalizácie a nerovnosť musí platiť)
- Ak nie je vhodné pridáme minimalizácii nové ohraničenie s poslednými získanými hodnotami v,w
- Opakujeme cyklus kým nemáme optimálne riešenie.
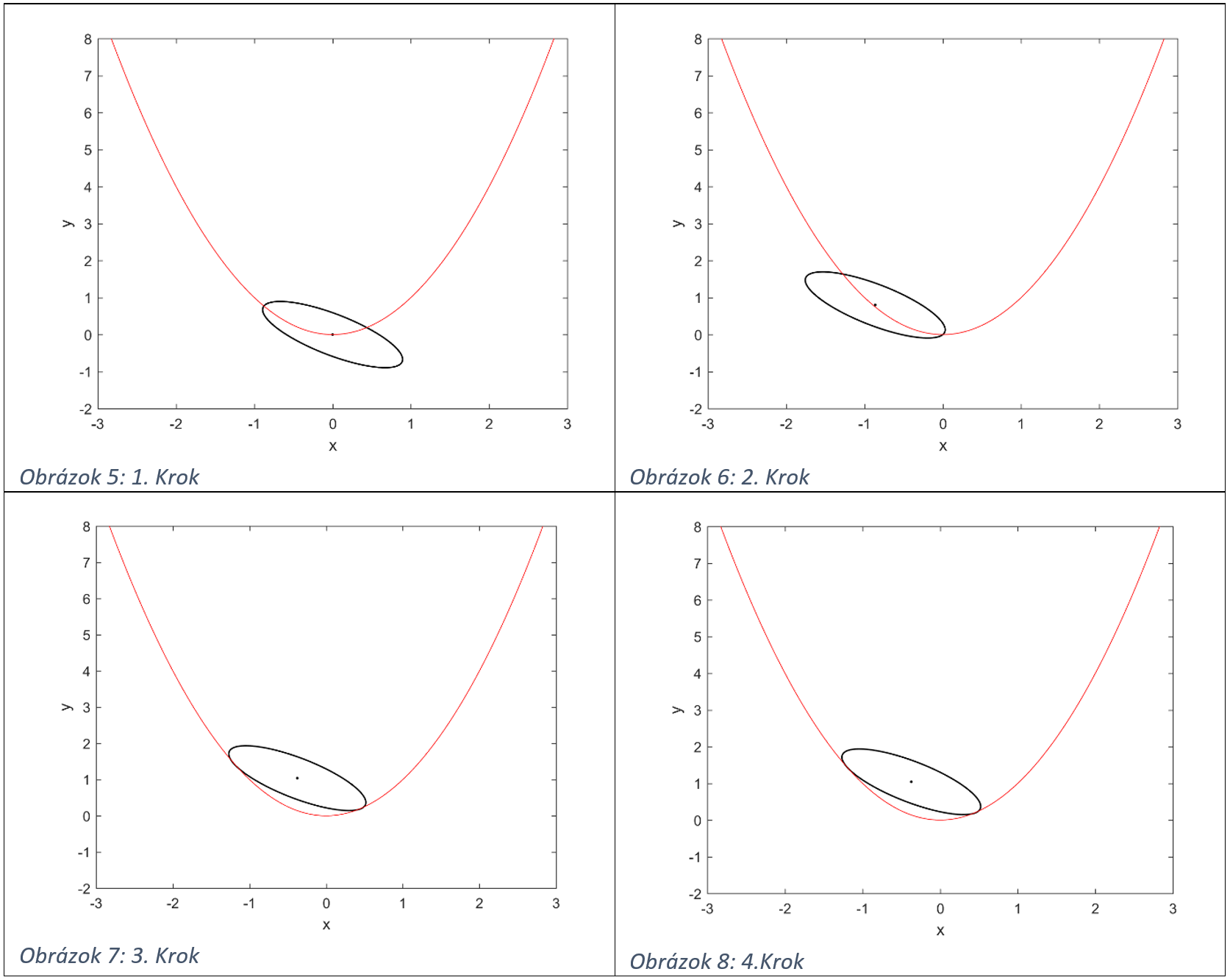
Po štvrtom opakovaní cyklu pri nástrele v=0 a w=0 sa cyklus zastaví, pretože sa našlo optimálne riešenie.
Pomocou druhej menovanej metódy sa mi podarilo nájsť najlepšie riešenie, teda elipsa je tak nízko ako sa len dá bez toho aby porušila ohraničenie dané parabolou. Je evidentné, že Blankenship a Falk metóda je vhodnejšia na riešenie tohto optimalizačného problému, pretože dosiahla optimálne riešenie a alternujúca nedospela výsledku, ktorý by sa aspoň vzdialene podobal na optimálne riešenie. Ponaučenie z optimalizácie pre šachistov: je dobré nájsť najlepší možný ťah v danom momente, ale je lepšie nájsť najlepší možný ťah v danom momente vzhľadom na všetky predchádzajúce a nasledujúce ťahy.
Literatúra:
[1] J. W. Blankenship, J. E. Falk, Infinitely constrained optimization problems, Journal of Optimization Theory & Applications 19 (2) (1976) 261–281.