Počas zimného semestra som sa vrámci semestrálnej práce venovala riadeniu laboratórneho inverzného kyvadla. Prácu by som rozdelila na 2 časti a to, riadenie uhla otočenia kyvadla pomocou viacerých riadiacich algoritmov a návrhu riadenia pre účely tzv. swing-up kyvadla.
Pod pojmom inverzné kyvadlo sa skrýva úloha, ktorú každý z nás sám vyskúšal a to napríklad balancovanie paličky na prstoch. A práve na tomto princípe funguje inverzné kyvadlo v praxi. Táto úloha je už vhodne aplikovaná vo svete techniky na výrobku osobného transportéru, tzv. segway. A možno nie každý z nás si uvedomil, že aj jazda na kolobežke je formou inverzného kyvadla, kde sa snažíme telo držať vo zvislej polohe a nespadnúť na zem počas jazdy.
Laboratórne inverzné kyvadlo je proces, pri ktorom sa vozík so závesným predmetom pohybuje po vodiacich lištách. Za pomoci remeňa umiestneného pri ozubených kolieskach a motora sa dá ovládať vozík oboma smermi. Kyvadlo sa následne pohybom vozíka rozkmitá, až sa dostane do vertikálnej polohy zo spodnej časti do vrchnej. Taktiež sa pohybom vozíka udržiava závesná časť v stabilnej vertikálnej polohe vo vrchnej časti tak, aby nespadlo nadol. Pomocou senzoru vieme merať uhol otočenia kyvadla, ale aj polohu vozíka.
V prvej časti svojho projektu som sa venovala návrhu riadenia uhla otočenia kyvadla pomocou zrýchlenia vozíka. Bolo použitých viacero algoritmov a to, PID riadenie (na grafe), kde sa regulátor navrhol na základe metódy umiestnenia pólov, následne sa použilo LQ riadenie a MPC riadenie.
Na grafe je zobrazená riadená veličina, theta, uhol otočenia kyvadla a riadiaca veličina, zrýchlenie vozíka.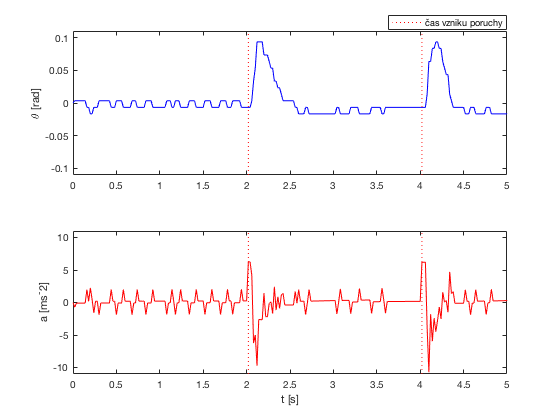
Najdôležitejšou časťou semestrálnej práce a neskôr aj diplomovej práce je tzv. swing up kyvadla, teda vyšvihnutie sa, kde sa kyvadlo budem snažiť dostať zo svojej prirodzene stabilnej vertikalnej polohy do nestabilnej vrchnej polohy a to pomocou MPC riadenia. Avšak riadenie takéhoto problému vôbec nie je také jednoduché ako predošlá časť a to z viacerých dôvodov:
- Model inverzného kyvadla je nelineárny a vyskytujú sa v ňom goniometrické funkcie
- Na vygenerovanie vhodného akčného zásahu je potrebné nájsť vyhovujúci solver.
Na vyriešenie tohto problému bol použitý napríklad solver fmincon, baron, casadi, ale nedokázali si poradiť s nelineárnym modelom a goniometrickými funkciami. Najreálnejší priebeh akčných zásahov nám poskytol toolkit ACADO (Automatic Control and Dynamic Optimization), avšak stále nie najvhodnejší na riadenie swing-up kyvadla.
A teda v najbližšom období sa budem venovať ladeniu váhových matíc MPC riadenia tak, aby kyvadlo vyletelo k nebesám 🙂