The aim of this project was to improve energy efficiency and control precision using modern identification and control strategies. In particular, the project compared a traditional modeling method (Strejc model) with a data-driven approach (Koopman model), and applied Model Predictive Control (MPC) to both.
Heat exchangers are often energy-intensive. By designing a smart controller, we can reduce energy waste and improve sustainability. Predictive control offers a powerful framework for this, especially when we use models that are built from real data.

To begin with, I identified the system using two different approaches. The Strejc model is a simple first-order approximation based on step responses. It is easy to interpret but assumes linear system dynamics. On the other hand, the Koopman model is a data-driven technique that uses neural networks to map the nonlinear behavior of the system into a higher-dimensional, so-called “lifted space,” where the dynamics become linear. In this space, the Koopman model produces matrices A, B, and C that define a linear state-space system. These matrices can then be used in predictive control.
The physical system used for testing was a plate heat exchanger from the laboratory. The input to the system was the percentage speed of the heating pump (5), and the output was the temperature of the water exiting the exchanger (1). Throughout the experiment, we performed 19 step changes in the pump speed, ranging from 20% to 100%. These data were then normalized and split into training and testing datasets.
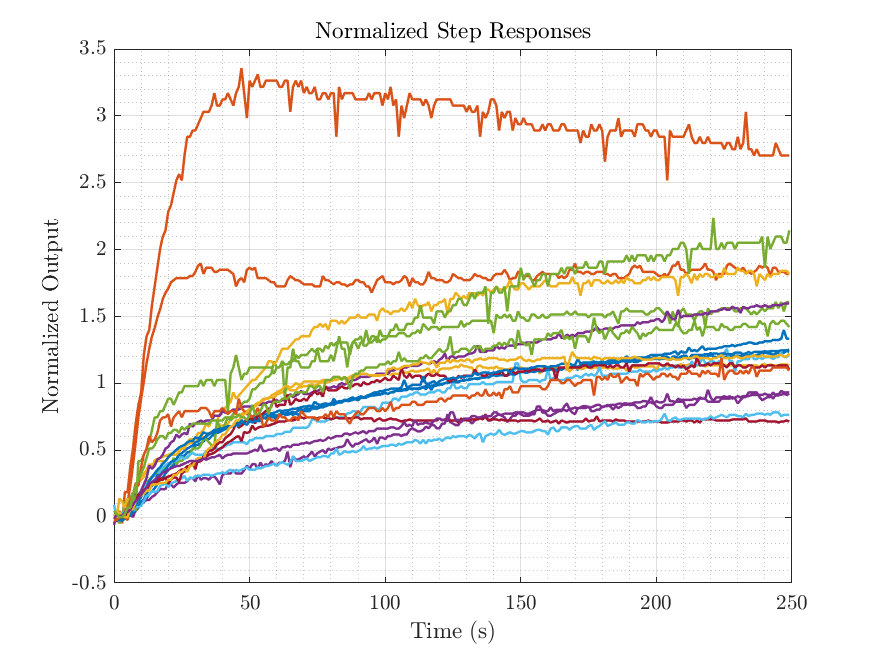
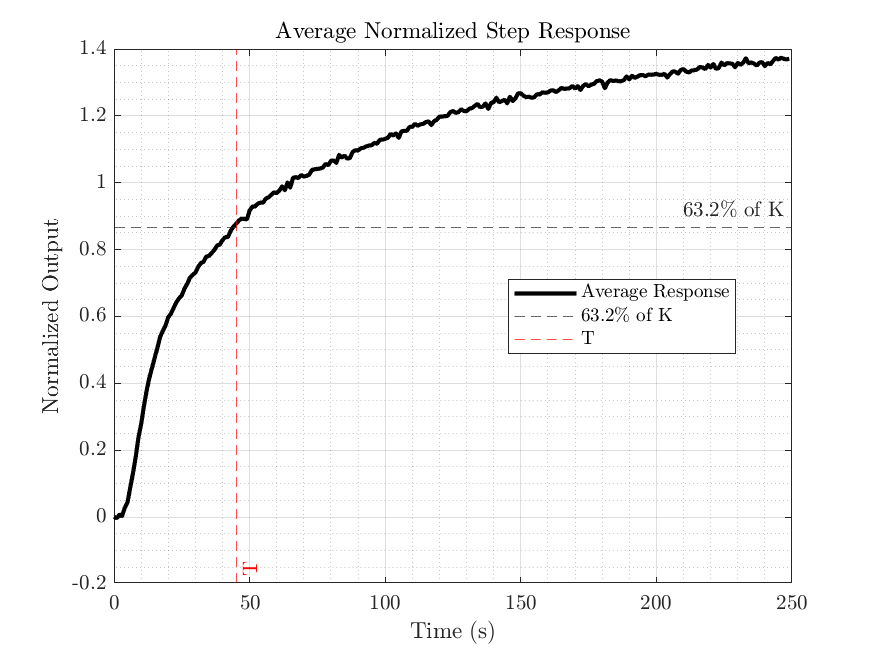
With the Strejc method, we calculated the average step response from the normalized data and extracted the system gain and time constant. The transfer function was then converted to a state-space model.
For the Koopman model, I used the Neuromancer framework in Python. It lifted the data into a 10-dimensional space and produced Koopman matrices A (10×10), B (10×1), and C (1×10). These matrices were optimized during training on scaled data using both the training and testing sets.
After both models were identified, I evaluated their prediction accuracy. The Koopman model achieved about 31% lower root mean squared error (RMSE) on test data compared to the Strejc model. This demonstrated its ability to capture the dynamics more precisely, especially during larger step changes.
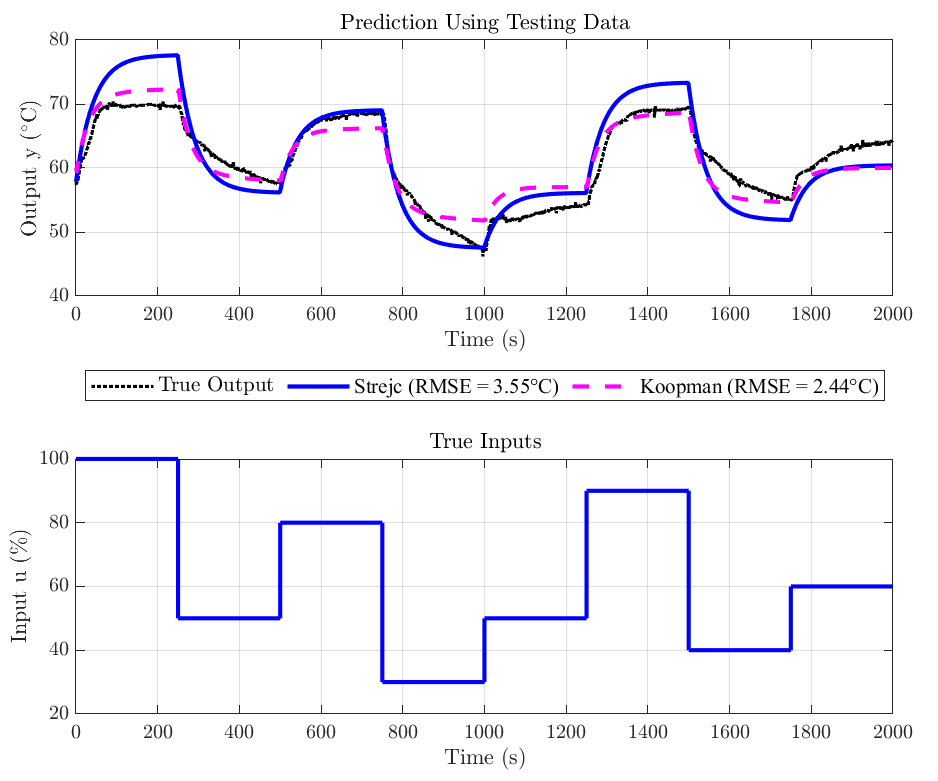
We then designed predictive controllers (MPC) using both models. The MPC was configured with a prediction horizon of 40 steps. The output and input were penalized with weights Qy = 10 and Qu = 1, respectively, prioritizing the tracking of the desired temperature. The control problem was solved using the YALMIP toolbox in MATLAB, with the quadprog solver. The input and output constraints were set based on the physical limits of the system, for example, the maximum output temperature was limited to 70 °C due to the hot water source averaging around 74 °C.
The simulation results showed that both controllers were able to steer the system to the desired steady-state. However, Koopman-based control produced a smoother control input and slightly lower RMSE. Although the Strejc model reached the steady-state faster, the Koopman controller was more accurate and gentle on the system.
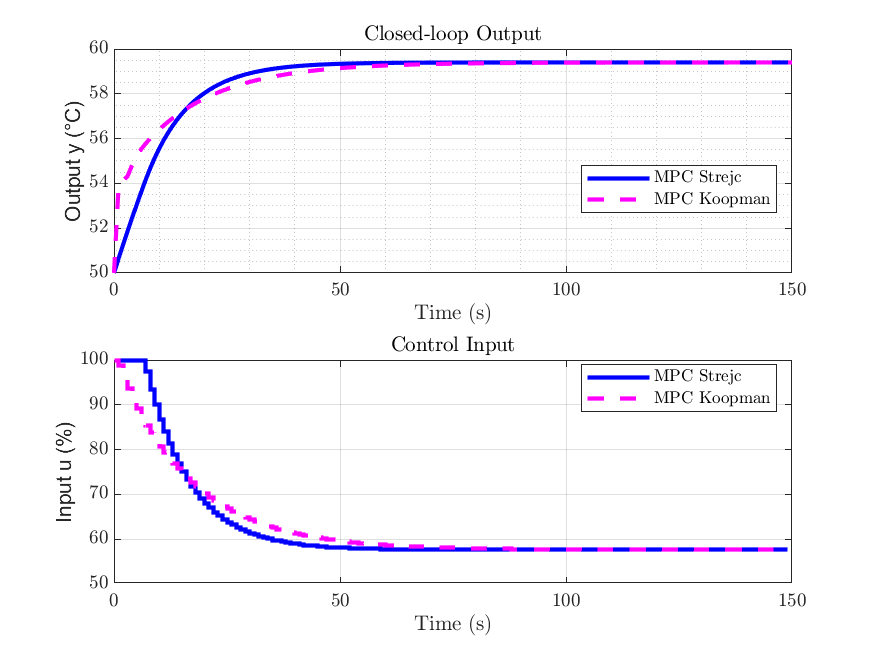
In terms of numerical performance, Koopman achieved lower RMSE, a lower value of the objective function, and reduced output deviations. The Strejc model required less control effort, but its predictions were generally less precise. These results highlight that Koopman-based control can be a strong alternative to traditional models when accuracy and robustness are important.
We also tested the controllers with a variety of initial conditions. Koopman consistently outperformed Strejc, especially when the system started far from the setpoint. This confirms its advantage for handling nonlinear systems over a wider operating range.
In the future, I plan to verify the Koopman controller on the physical device and compare its performance with other data-driven models. I also hope to extend the control structure to multi-input systems, possibly including the cold water pump as an additional actuator.