Predstavme si, že vo fabrike dôjde k nečakanému úniku plynu. Nájdenie miesta, kde k tomuto úniku došlo, nemusí byť ľahké a hlavne je to často časovo náročné. Okrem toho si musíme uvedomiť, aké straty by to pre podnik znamenalo. Nie len zastavenie prevádzky, či stratu suroviny na beh procesu, ale aj ohrozenie ľudí a životného prostredia. Takýto problém by sme mohli riešiť využitím robotického zariadenia, ktoré by bolo schopné autonómne nájsť toto miesto úniku. A práve týmto, tvorbou algoritmu na riadenie pohybu robota v priestore, sa zaoberala moja bakalárska práca.
Najprv si musíme uvedomiť, ako to vyzerá v takej miestnosti, kde dôjde k úniku plynu. Koncentrácia plynu je v každom mieste priestoru iná a to je faktor, ktorý dokážeme využiť pri robotickej optimalizácii. Robotom sme vždy schopní merať danú fyzikálnu vlastnosť iba v jednom mieste a na základe tohto údaja vyhodnotiť nasledovný krok.
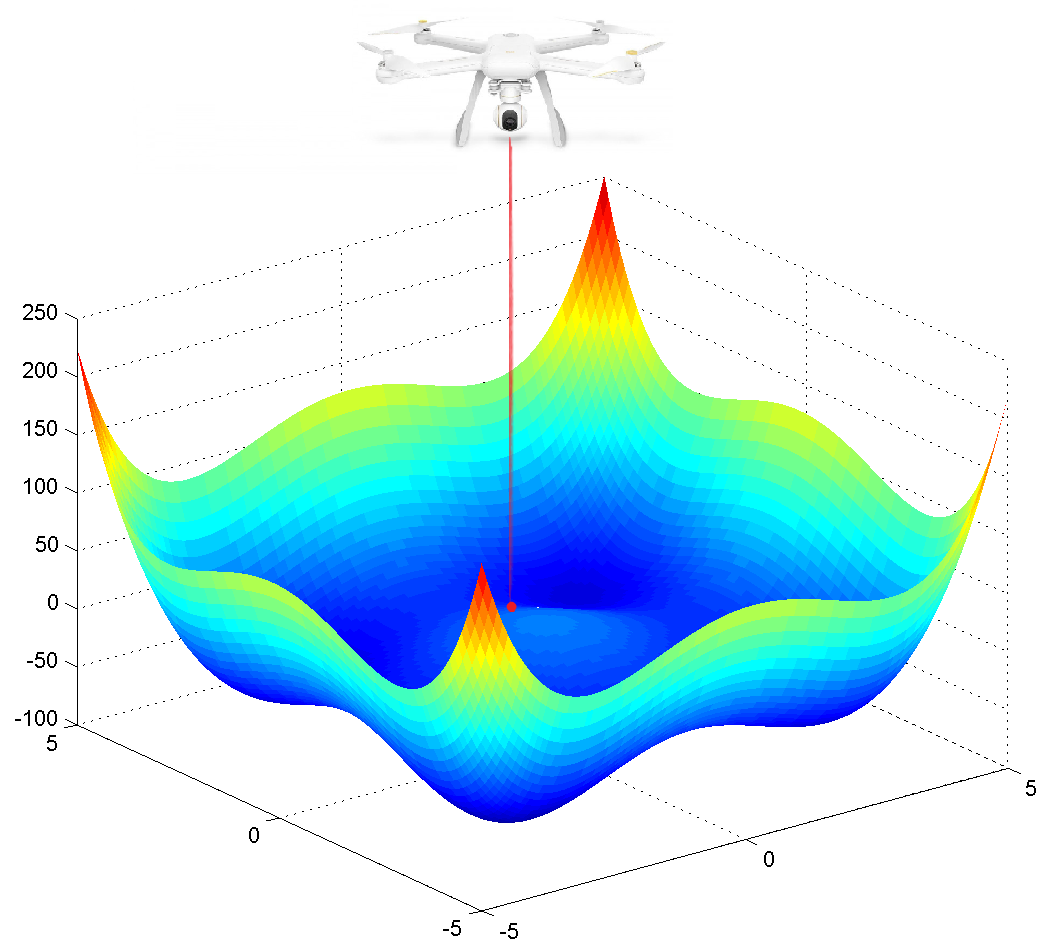
V mojej práci som pracovala s kontúrovým grafom funkcie, ktorý predstavuje vývoj fyzikálnej vlastnosti v priestore. Ponad graf sa pohyboval senzor svietivosti umiestnený na plottri, ktorý meral hodnotu funkcie v danom mieste priestoru. Úlohou bolo nájsť minimum (alebo maximum) funkcie na takomto kontúrovom grafe. Riešime teda optimalizačný problém minimalizácie funkcie. Z matematiky už vieme, že optimum funkcie dokážeme nájsť pomocou derivácie resp. gradientu funkcie. Ale čo robiť, ak predpis funkcie nepoznáme a teda nepoznáme ani jej derivácie?

Existuje mnoho numerických metód, ktoré si dokážu s týmto problémom poradiť. V mojej práci som pracovala s dvoma typmi metód. Prvou skupinou metód boli bezgradientové techniky. Ich princíp je nasledovný. Robot v danom začiatočnom bode odmeria hodnotu fyzikálnej vlastnosti, akú v priestore skúmame a zapamätá si ju. Nasledovne sa náhodne vygeneruje ďalšie miesto v priestore, kam sa robot presunie a odmeria novú hodnotu. Následne porovná funkčnú hodnotu v pôvodnom aj novom mieste a rozhodne sa, ktorá z nich je lepšia (pri minimalizácii je to tá menšia). Vzhľadom na toto porovnanie algoritmus vyhodnotí, aké bude ďalšie správanie sa robota v priestore. Tento presun je znázornený na obrázku nižšie.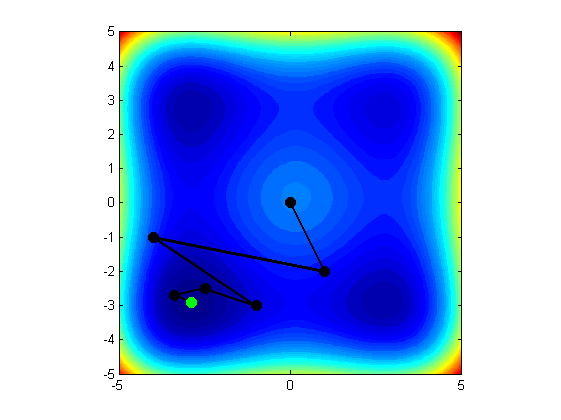
Druhou skupinou metód, sú techniky založené na odhade gradientu. Keďže matematicky presný gradient funkcie v bode nepoznáme, musíme pracovať iba s funkčnými hodnotami v okolí skúmaného bodu, ktoré získavame zo senzora. Ich porovnávaním a následným spracovaním, je algoritmus schopný vyhodnotiť smer lokálneho klesania v okolí týchto bodov. Následne sa robot posúva v tomto smere, čím sa dostáva do minima (obrázok nižšie).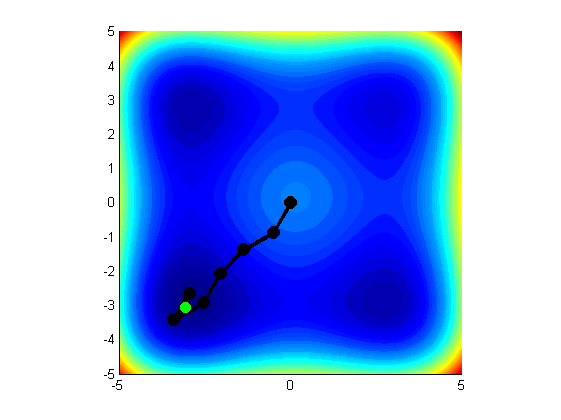
Všetky tieto metódy som aplikovala na priestor bez prekážok, ktorým by sa robot mal vyhnúť. Prípady, kedy sa takéto prekážky v priestore vyskytovali, som riešila pomocou bariérovej logaritmickej metódy, vďaka ktorej som na funkčné hodnoty v bodoch blízko takýchto prekážok uložila penalizáciu a teda ich funkčná hodnota zaznamenaná algoritmom bola oveľa vyššia ako reálna. Vďaka tomu, dochádza k akejsi úprave funkcie, pomocou ktorej sa robot dokáže vyhnúť tejto prekážke.
Takýmto spôsobom (s prekážkami, či bez nich) by sme mali byť schopní veľmi rýchlo detekovať miesto úniku plynu a znížiť peňažné straty podniku, ale aj dopad na životné prostredie.