V našom obore sa stretávame s mnohými úlohami, ako napríklad riadiť systém, odstraňovať poruchy ovplyvňujúce zariadenie, či dokonca musíme odhadovať veličiny procesu, ak ich nemáme k dispozícii. Tieto úlohy a všetko, čo je s nimi spojené sú závislé na jednej rovnakej veci a to je model systému. Ak máme dostatočne presný model, ktorý nie je komplikovaný a zároveň dobre opisuje dynamiku systému, môžeme podľa neho navrhnúť vhodné riadenie, alebo odhad stavov.
Hlavným cieľom môjho projektu bolo nájsť takýto nelineárny model, ktorý bude spĺňať všetky podmienky. Vo všeobecnosti sú dve metódy, ako sa dostať k takémuto modelu:
- Dokonale poznať systém a prírodné zákony, podľa ktorých sa náš systém správa. To dosiahneme zostrojením materiálových a entalpických bilancií systému, ktoré budú predstavovať náš model. Inak povedané, urobíme si všetko sami.
- Využiť počítač, optimalizáciu a matematiku. Inak povedané počítač to spraví za nás.
Keďže sme na ústave automatizácie a informatizácie a lenivý automatizér je dobrý automatizér, zvolil som si druhú metódu. Zo skúsenosti som vedel, že práve neurónové siete sa budú na takýto problém hodiť.
Neurónové siete generujú požadovaný výstup zo vstupných informácií. Kostru neurónovej siete prestavuje súbor takzvaných neurónov, ktoré pričítavajú posun a pomocou váh násobia vstupný signál, ďalej ho vynásobia aktivačnou funkciou, ktorá povie, do akej miery je neurón aktívny. Aby bola neurónka funkčná, musí sa najskôr natrénovať na trénovacích údajoch. Na základe vstupu a požadovaného výstupu spustíme optimalizáciu, ktorá nájde vhodné váhy a posuny, aby neurónka obsiahla závislosť, ktorá je skrytá za týmito údajmi.
Práve táto vlastnosť, pomocou ktorej nájdeme závislosť medzi vstupom a výstupom neurónovej siete, bola klúčová v mojom projekte. Pomocou programovacieho jazyka Python a knižnice TensorFlow (určená pre programovanie strojového učenia) som naprogramoval upravenú neurónovú sieť. Nahradil som v nej aktivačné funkcie matematickými operáciami ako je násobenie, delenie, odmocniny, sínus a podobne. Potom som z neznámeho systému vygeneroval trénovacie údaje pre neurónku. Vstupom do neurónky boli vstupy a stavy systému, ktoré sa majú objaviť v našom modeli. Výstup z neurónky bol komplikovanejší, potreboval som ku každému stavu jeho deriváciu. Mal som dve možnosti, buď by som využil aproximáciu derivácie, čo by zanieslo miernu chybu do našich údajov, alebo by som využil jedinú známu hodnotu derivácie, a to v ustálenom stave, kde je rovná nule. Kedže kvalita neurónky je závislá od kvality dát, zvolil som druhú možnosť. Na základe týchto údajov som mohol začať trénovanie neurónky, ktoré bolo založené na troch fázach.
- Nájsť vhodný nástrel.
- Vylúčenie matematických operácií, ktoré sa nenachádzajú v modeli.
- Optimalizácia konštánt.
Po takomto tréningu sme splnili stanovený cieľ: celá kostra neurónky predstavuje náš hľadaný model systému. Výhodou je, že takto skonštruovaný program stačí len mierne upraviť a môžeme ho využívať pri hocijakom systéme, vždy nám nájde najpresnejší model vzhľadom k zadaným matematickým operáciám. Dá sa využívať aj v prípade, ak model poznáme a neznáme sú len konštanty (súčiniteľ prestupu tepla, konštanta ventilu atd.). V takom prípade zadáme len tie matematické operácie, ktoré sú v modeli a daný program nájde vhodné konštanty.
Celý tento postup som aplikoval na systéme dvoch zásobníkov kvapaliny s interakciou.
Skutočný model:
ẋ1 = 1,667 ∙ q0s – 1,5 ∙ √(h1 – h2)
ẋ2 = 1,125 ∙ √(h1 – h2) – 1,25 ∙ √(h2)
Nájdený model:
ẋ1 = 1,665 ∙ q0s – 1,717 ∙ √|0,7538 ∙x1 – 0,7511 ∙ x2|
ẋ2 = 0,765 ∙ √|0,7538 ∙ x1 – 0,7511 ∙ x2| – 1,06 ∙ √|0,2216 ∙ x1 – 0,9872 ∙ x2|
Na prvý pohľad sa môže zdať, že model nie je presný, ale pri simuláciách zistíme opak. Nájdený model je presný a má len nepatrné odchýlky od skutočného systému.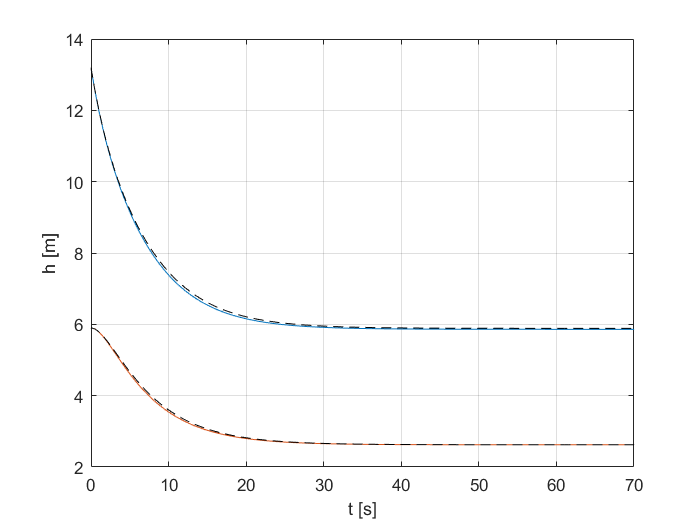
Obr.1 porovnanie PCH nájdeného modelu (čierne) a skutočného systému
V druhej časti môjho semestrálneho projektu som sa venoval návrhom nelineárneho odhadu stavov, o ktorých nemáme informácie. Takýto odhad môže ušetriť firme veľké náklady za nákup a údržbu drahých senzorov.
Náš nelineárny odhad bude opäť predstavovať neurónka. Rovnako ako klasický lineárny odhad, aj náš nelineárny berie ako vstupné údaje vstup a výstup zo systému. Z experimentov som prišiel na to, že ak ako vstup do neurónky využijem aktuálny vstup a výstup plus tri minulé hodnoty vstupu a výstupu zo systému, náš odhad bude oveľa presnejší. Keďže pri reálnych systémoch máme k dispozícií signál iba v určitých periódach, musel som pracovať s diskrétnym systémom. Následne som neurónku parametrizoval periódou vzorkovania Ts, takže odhad funguje pri rôznych periódach vzorkovania. Trénovacie dáta som získal z uzavretého regulačného obvodu s PID regulátorom.
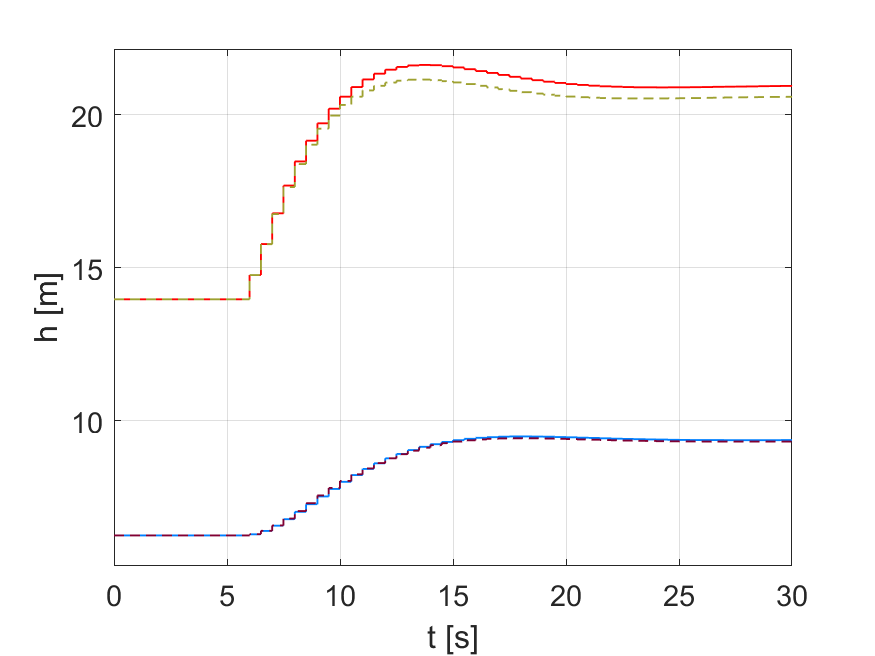
Obr.2 lineárny odhad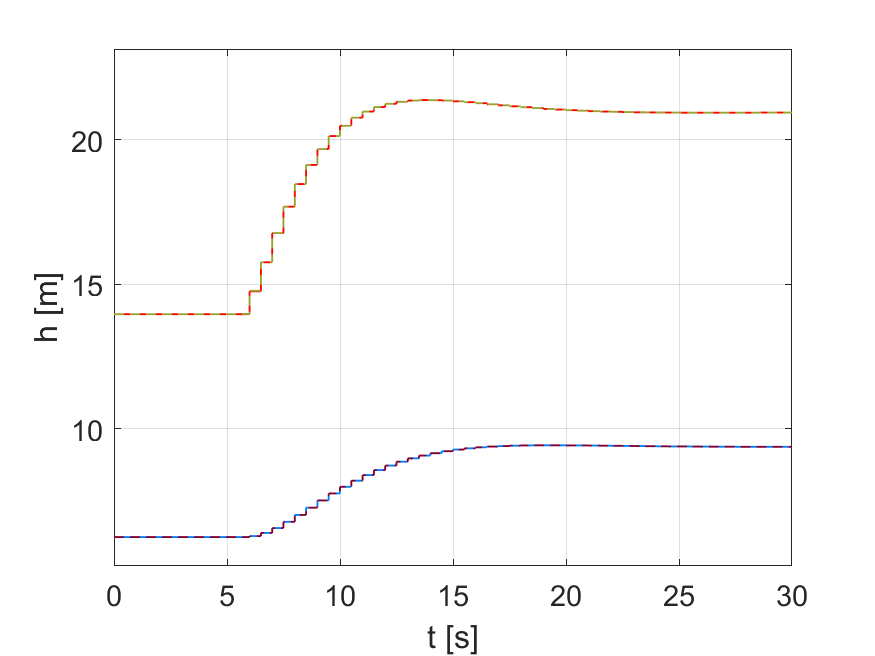
Obr.3 nelineárny odhad
Z obr. 1 a 2 vidíme, že nelineárny odhad funguje na 100% oproti lineárnemu, ktorý je založený na zjednodušenom modeli a má odchýlky od skutočného systému.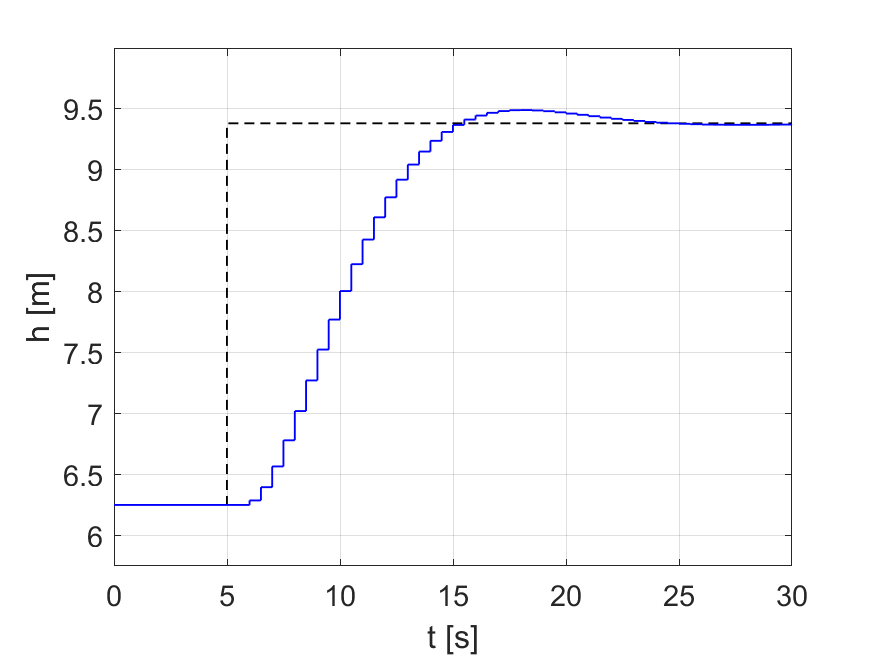
Obr.4 riadenie s lineárnym odhadom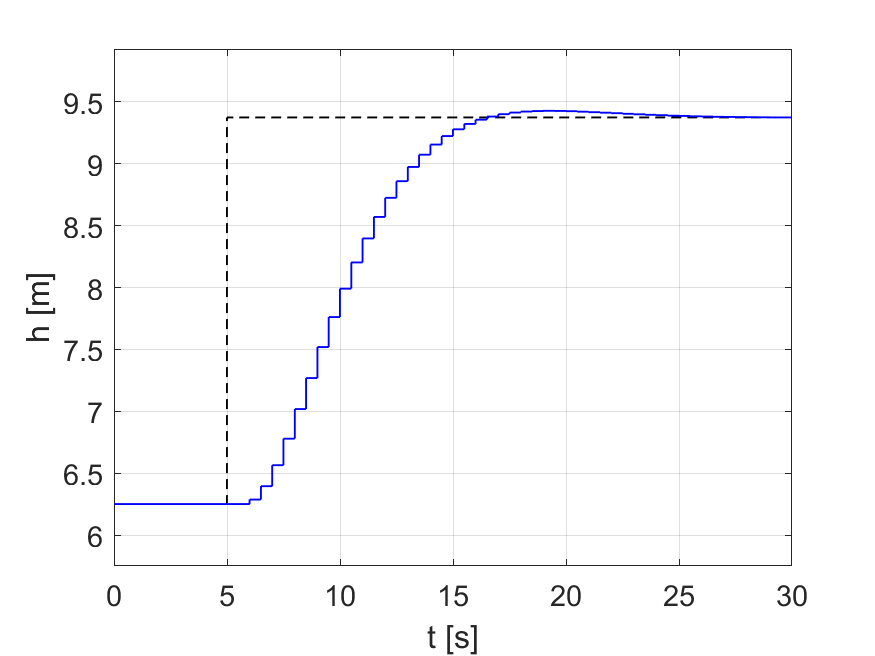
Obr.5 riadenie s nelineárnym odhadom
Ako môžme vidieť, pri použití nelineárneho odhadu stavov sa zlepšilo aj celkové riadenie.