Humankind considers (rightfully?) itself to be the most intelligent entity. It is so intelligent to find out that brains, which are composed of neurons are responsible for that intelligence. And what these smart humans do when they want to create a non-natural, artificial intelligence? They copy a mechanism from their own brains. Isn’t that an ingenious idea? Yes, it is. Does it work? Well…

I will try to keep an explanation of neural networks (NN) in this post brief and not very exhaustive, although there are a lot of things to be said. A main ability of the artificial neural network is to find (by learning) a relation between the input and output values. Then, the neural network can apply acquired knowledge to other input data and solve problems such as classification and thus recognition, regression and thus prediction, or much more. But how can a neural network do that?
An artificial neural network consists of neurons. A neuron can have many inputs, but usually one output. It can process and transfer information. In NN neurons are organized consecutively and in layers, where the information can move in only one direction. There is one input layer, one output layer and one or more hidden layers. The neural network can be described as an oriented graph, where nodes are neurons and edges are connections.
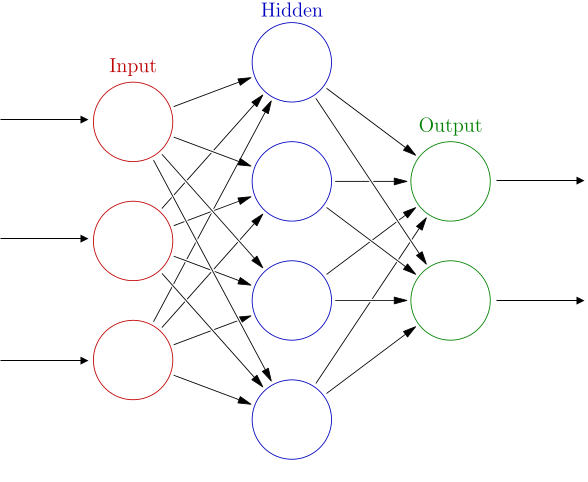
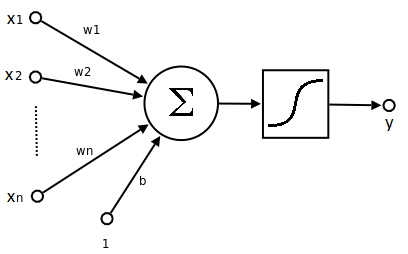
The neuron as an elementary unit of the NN is in fact a mathematical function. It takes inputs, which are weighted outputs $(x_i\cdot w_i)$ from all neurons in the previous layer and sums them together with bias $b$. Then the sum is passed into the nonlinear activation function $f$, which usually has a sigmoid shape to return values ranging from 0 to 1. This value $y$ is (after multiplying by its weight $w$) passed to all neurons in the next layer.
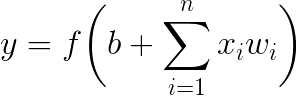
The purpose of a training process consist in finding proper values of weights and biases. In supervised learning, the right output labels Y that correspond to predictors X are known. At first, a network computes the preliminary output, which is compared with the true output. The goal is to minimize that difference by adjusting weights and biases. An error is spread in backward propagation and weights are optimized by gradient descent algorithm.
After training (which usually takes some time) the neural network is prepared to predict a new results. If the neural network is trained well, the results can be excellent, but the NN doesn’t give us an explanation why is this particular output an answer. A relation between the weights and the dataset remains as mystery and we are not able to fully open that black-box.

Let’s create one NN, in the MATLAB with Neural Network Toolbox it is easy. We will use our familiar wine dataset again. At first, we load data and divide them into training and testing, into predictors X and labels (classes) Y.
%% loading and splitting data
file_name = 'wine.data';
data = csvread(file_name);
percentage_of_training_data = 0.7;
[training_x, training_y, testing_x, testing_y] = split_data(data, ...
percentage_of_training_data);
The neural network needs data organized in a way where each sample is in the column and attributes are in the rows. The output classes must be transformed into a binary matrix, where position of 1 corresponds to the class number. Illustration:
1 0 0
1 --> 0 2 --> 1 3 --> 0
0 0 1
This transformation can be done in MATLAB in two ways shown below. A number of classes also define a number of neurons in the last, output layer.
%% data preparation
Xnet = training_x';
number_of_classes = 3; %
Ynet = zeros(number_of_classes,size(training_x,1)); % these steps could
for i = 1:number_of_classes % be replaced by:
idx = find(training_y==i); % Ynet =
Ynet(i, idx) = 1; % dummyvar(training_y)'
end %
Number of neurons in the hidden layer was set to 5 and then we can train the neural network by a MATLAB function train.
%% defining the size of NN
hiddenLayerSize = 5;
net = patternnet(hiddenLayerSize);
%% training NN
tnet = train(net, Xnet, Ynet);
And that's all we need, it also shows a created network. It has 13 input neurons, each of them belongs to one wine attribute.
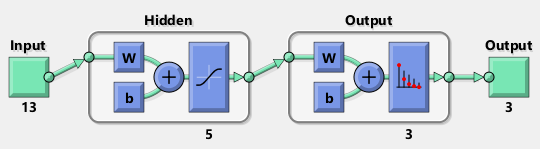
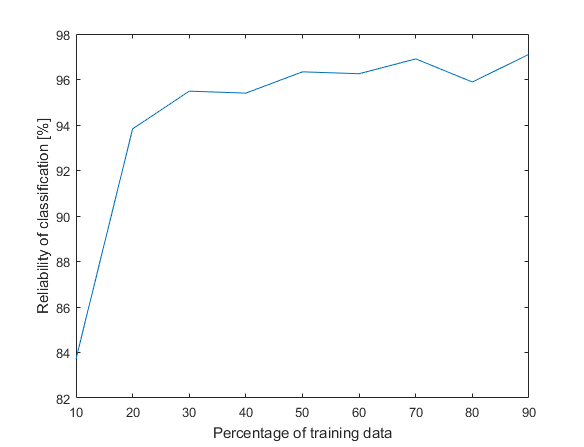
The created network already divides provided data into training, testing and validation data, thereby the network can evaluate itself. But at the beginning, we put 30 % of samples aside, so we can calculate a reliability of trained network also manually.
%% manual validation
for i = 1:size(testing_x,1)
x = testing_x(i, :)';
ynn = sim(tnet, x);
[yconfidence, ypred] = max(ynn);
yprediction(i) = ypred;
end
number_of_errors = nnz(testing_y'-yprediction);
reliability = (size(testing_x,1)-number_of_errors)/size(testing_x,1)*100
30 % from the dataset is 53 samples, 2 from these 53 testing samples were classified incorrectly, so we achieved 96.2 % reliability. Not bad. We don’t even have to wait long, creating a network model for this particular dataset takes only 1.3 seconds. By altering the ratio between size of the training and the testing data and by calculating an average reliability for each percentage, we can plot them in the graph. As we expect, increasing the amount of training data also increases reliability.